УДК 537.226.33
ТЕМПЕРАТУРНЫЙ ГИСТЕРЕЗИС В СЕГНЕТОЭЛЕКТРИКЕ KDP С УЧЕТОМ ГЕТЕРОФАЗНЫХ ФЛУКТУАЦИЙ
© 2004 г. И. Е. Петров sРезультаты изучения сегнетоэлектрика KDP (дигидрофосфат калия) показывают существование зависимости между температурным гистерезисом и величиной плотности поверхностной энергии зародышей сегнетофазы s. Особенность приведенного метода заключается в том, что мы сравниваем модельные предсказания с экспериментальными результатами с тем, чтобы выразить s, т.е. s считаем свободным параметром. Этот подход отражает трудность предсказания значений s из теоретических расчетов любого вида. В последнее время механизм зародышеобразования успешно используется при описании фазовых переходов первого рода в различных системах.В статье приняты сокращения:
s – плотность поверхностной энергии;ГТФ – гетерофазные флуктуации;
ФП1 – фазовый переход первого рода (ФП2 – соответственно, второго рода);
ФП 1>2 - фазовый переход из фазы 1 в фазу 2 (аналогично, ФП 2>1 - из фазы 1 в фазу 2);
СЭ – сегнетоэлектрик;
СФ – сегнетофаза;
ПФ – парафаза;
ТДП – термодинамический потенциал.
О переохлаждении и о температурном гистерезисе можно говорить лишь в отношении ФП1. При ФП2 их нет.
Долгое время считалось, что в СЭ KDP происходит ФП2, но измерения коэффициента разложения ТДП b показали, что b<0, что является признаком ФП1. Более тщательные измерения поляризации P вблизи точки Кюри (Tk) показали, что имеет место небольшой скачок P в точке Tk. Это подтвердило тот факт, что имеем дело с ФП1.
После этого был зафиксирован температурный гистерезис. Существование температурного гистерезиса является следствием того, что существует метастабильное состояние фазы.
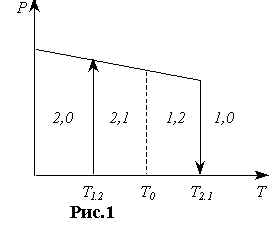
Пусть T0 – температура фазового равновесия (иногда ее называют Tk). При увеличении температуры до T21 происходит ФП 2>1 (из СФ в ПФ). При температуре T12 происходит переход ФП 1>2 (см. рис.1).
В области T>T21 существует только фаза 1 (фаза 2 не может существовать даже как метастабильная). В области T0<T<T21 фаза 1 устойчива, но здесь может существовать как метастабильная фаза 2. Аналогично, в области T12<T<T0 устойчивая фаза 2, метастабильная – 1, в области T<T12 существует только фаза 2.
Таким образом, температура фазового перехода ФП 2>1 T21 – это температура, при которой исчезает метастабильное состояние СФ.
Теоретический расчет дает: температурный гистерезис для KDP DT=T21-T12= 4•10-2 K. Переохлаждение T0-T12=3•10-2 K, перегрев- 1•10-2 K. Но, согласно экспериментальным данным
DT=2•10-2 K, то есть ФП начинается раньше, чем исчезает метастабильное состояние исходной фазы. Это обстоятельство указывает на необходимость учета флуктуационных явлений. ФП происходит с преодолением потенциального барьера (см. рис.2). Система берет для этого энергию за счет тепловых флуктуаций (энергия теплового движения порядка kT).
На рис.1 по оси ординат откладывается Р - спонтанная поляризация, по оси абсцисс – температура T. Спонтанная поляризация отлична от нуля, когда СЭ находится в СФ. Область 2,0 –это область, в которой может существовать только фаза 2; в области 2,1 фаза 2 устойчивая, а фаза 1 метастабильная. В области 1,2 устойчивая фаза 1, метастабильная – 2, в области 1,0 может существовать только фаза 1.
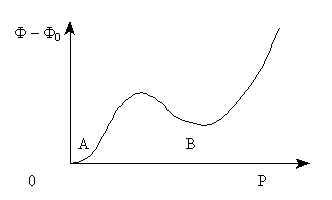
Рис. 2
На рис.2 показана зависимость изменения ТДП относительно ТДП СФ Ф0 , который одновременно является нулевым членом разложения ТДП (об этом ниже), от величины спонтанной поляризации P. В ПФ P=0 (точка А на графике), в СФ P отлична от нуля, при этом относительный минимум энергии на графике показывает метастабильность СФ (точка В), тогда как точке А соответствует абсолютный минимум энергии, что указывает на устойчивость ПФ.
(Изображена только часть графика. График симметричен относительно оси ординат).
ФП происходит не сразу во всем кристалле. По мере приближения к температуре ФП в кристалле флуктуационно возникают и исчезают малые области другой фазы (ГТФ). По мере приближения к температуре ФП число этих флуктуаций растет. В самой точке ФП эти области новой фазы занимают примерно половину кристалла, начинается слияние этих областей, в результате чего происходит быстрый ФП.
Первым о зародышах новой фазы заговорил Френкель, экспериментально наблюдал их Кенциг. Важнейшие характеристики зародышей – число частиц в зародыше g и плотность поверхностной энергии s. Одна из задач теории – нахождение этих параметров. Экспериментальное нахождение
s почти неразрешимая задача.Существует несколько способов оценки величины
s. В теории Ландау для ФП1 ТДП раскладывается в ряд следующим образом (спонтанная поляризация изменяется скачком, поэтому нельзя считать, что вблизи ФП P имеет маленькое значение, а значит нельзя ограничиваться 4-ой степенью разложения):![]() (1)
(1)
Условие равновесия - минимум Ф: ![]() ;
; 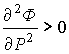 . Это
условие позволяет установить зависимость a от Т, а также связать
максимальное значение спонтанной поляризации в
СЭ Р0 с коэффициентами b и g.
. Это
условие позволяет установить зависимость a от Т, а также связать
максимальное значение спонтанной поляризации в
СЭ Р0 с коэффициентами b и g.
В случае образования зародыша СФ поляризация в объеме вещества будет иметь разные значения (см. рис.3): внутри зародыша P=P0, вне - Р=0. В этом случае
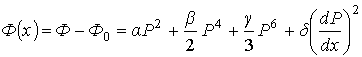 (2)
(2)
где d – корреляционный коэффициент.
А ТДП во всем объеме кристалла
(представляющем собой цилиндр, ось которого
совпадает с осью х, и с площадью основания, равной
единице)-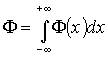 . Для
нахождения реальной зависимости Р(х) нужно
решить задачу о нахождении минимума Ф или
минимума функционала:
. Для
нахождения реальной зависимости Р(х) нужно
решить задачу о нахождении минимума Ф или
минимума функционала:
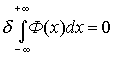 (3)
(3)
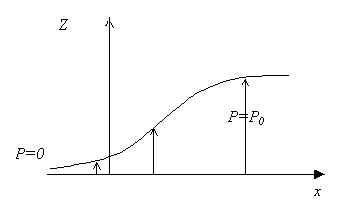
Рис. 3
Благодаря полной математической
аналогии между этой задачей и задачей
классической механики о нахождении экстремали
функционала действия, мы можем воспользоваться
уже существующим решением подобного в
математическом плане типа задач. Получим: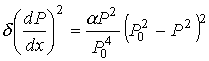 . Отсюда найдем
зависимость Р(х):
. Отсюда найдем
зависимость Р(х):
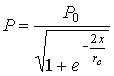 (4)
(4)
где 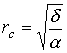 - так
называемая эффективная толщина стенки зародыша.
- так
называемая эффективная толщина стенки зародыша.
Вычисление плотности поверхностной энергии осуществляется по формуле
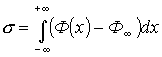 (5)
(5)
где ![]() -
потенциал однодоменного кристалла, т.е. в случае,
если стенка “удалена на бесконечность”, дает
значение s:
-
потенциал однодоменного кристалла, т.е. в случае,
если стенка “удалена на бесконечность”, дает
значение s: 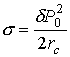 . Для приближенной оценки d
предположим, что корреляционная энергия
. Для приближенной оценки d
предположим, что корреляционная энергия![]() одного порядка с
объемной энергией
одного порядка с
объемной энергией ![]() при
температуре Т12, т.е.
при
температуре Т12, т.е. ![]() .
.
Произведем вычисления: ![]() ;
; ![]() (в
единицах гауссовой системы). В этом приближенном
оценивании нас интересует порядок величин.
(в
единицах гауссовой системы). В этом приближенном
оценивании нас интересует порядок величин.
Описанный выше способ вычисления
s является непосредственным. Существует и способ косвенной оценки s.Динамика ФП1 следующая. Рассмотрим систему пар- жидкость. Если очень осторожно охлаждать очень чистый пар, то при прохождении Т0 пар остается (в метастабильном состоянии). При температуре Т12 происходит ФП 1>2. При этом приращение ТДП
![]() (6)
(6)
где А и В – коэффициенты Френкеля.
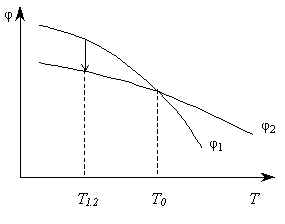
Рис.4
Если бы мы не учитывали поверхностное натяжение, то при переходе одной молекулы из фазы 1 в фазу2 приращение потенциала равно j2 –
j1 (речь идет об удельном ТДП, т.е. о химическом потенциале j), если g молекул испытывают ФП, то g•(j2 – j1). Сравнивая с (6), получаем![]() (7)
(7)
Вблизи Т0 (где
j1 = j2) B=0. Разложим в ряд по степеням DТ, ограничившись первой степенью разложения:l
>0). Тогда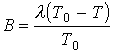 (8)
(8)
Второе слагаемое в формуле (6) есть поверхностная энергия. Энергия поверхностного натяжения (на капле)
![]() (9)
(9)
где Sп – площадь поверхности
сферической капли, R – ее радиус. Объем зародыша с
одной стороны равен V0•g , а с другой - ![]() . Из равенства
. Из равенства ![]() можно выразить R и
подставить в (9) :
можно выразить R и
подставить в (9) :
![]() (10)
(10)
где ![]() .
Сравнивая с (6), получаем:
.
Сравнивая с (6), получаем:
![]() (11)
(11)
Указанное значение С верно для сферической формы зародыша. Для других форм значение С иное, однако, формулы (10),(11) остаются справедливыми.
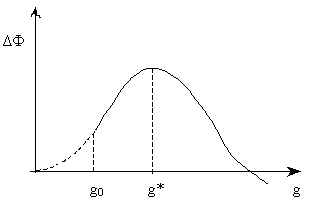
Рис.5
График зависимости DF от g приведен на рис.5. Исследуем функцию
DF(g) на экстремум: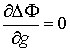 .Отсюда
.Отсюда
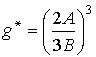 (12)
(12)
g* - критический размер зародыша. Если флуктуационно возникнет зародыш размером g<g*, то ему энергетически выгодно исчезнуть (см. рис.5), если размер зародыша g>g*, то ему выгоднее расти (при этом наступает ФП).
g* зависит от температуры. Подставим (11), (8) в (12):
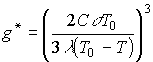 (13)
(13)
Из этой формулы видно, что ФП1 обязательно связан с перегревом или переохлаждением системы. Если перегрева нет (Т=Т0), то g*= Ґ - ФП не наступит никогда (невозможно реализовать условие g>g*).
Флуктуационно возникает зародыш размером g0 (для СЭ KDP g0»103). Чем дальше от Т0, тем меньше критическое значение g* (см. (13). Если g* станет равным g0 (уже существующему, флуктуационно образовавшемуся зародышу), то произойдет ФП. Т.е. условие ФП:
![]()
Связывая (17) и (16) и выражая s, получим значение плотности поверхностной энергии, вычисленное косвенным способом:
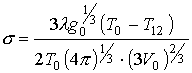 (15)
(15)
Формула (15) позволяет оценить s, определив на практике величину переохлаждения (или величину гистерезиса).
Расчет дает при косвенной оценке ![]() (эрг/см2), что по
порядку величины полностью согласуется со
значением
(эрг/см2), что по
порядку величины полностью согласуется со
значением
Вывод:
ЛИТЕРАТУРА
The temperature gysteresis of segnetoelectric KDP with consideration of heterophase’s fluctuations
The research’s of segnetoelectric KDP (kalium dihydrophosphat) results show the existence of dependence of temperature gysteresis from value of surface energy’s density of segnetoelectric’s clusters s . The specific of given method consist in fact that we compare model’s conclusions with experienced results to find s , so we consider s like free parameter. This method reflects a difficulty of estimation of s from any theoretical calculation. In recent years the theory of clusters appearance is used successfully for the description of phase’s transitions of the first kind in different systems.
Кафедра медицинской биологической физики
Смоленская государственная медицинская академия
Поступила в редакцию 19.12.2003.