ТЕОРИЯ
СИММЕТРИИ И МОРФОЛОГИЯ
УДК 51
Лекция
ГРУППЫ
И ГОМОМОРФИЗМЫ
© 1997 г. Е. П.
Емельченков, В. Е. Емельченков
В работе
рассматриваются два важных понятия
теории групп (нормальный делитель и
фактор-группа) и доказываются две
теоремы - теорема Лагранжа и
теорема о гомоморфизмах групп. В
теореме Лагранжа выясняется, каким
может быть порядок произвольной
подгруппы конечной группы. Теорема
о гомоморфизмах дает исчерпывающее
описание всех групп, на которые
может гомоморфно отображаться
произвольная группа.
Пусть G=
<G; ?> - некоторая группа, и H=
<H; ?> - подгруппа группы G.
С помощью подгруппы H на множестве G
элементов группы G можно
определить бинарное отношение :
для любых двух элементов a и b
из G
в том и только в том случае, если в H существует такой элемент h, что выполняется равенство
.
Теорема
1.1. Отношениеявляется
отношением эквивалентности на
множестве G.
Доказательство.
Для доказательства надо показать,
что отношение рефлексивно,
симметрично и транзитивно.
1)
Рефлексивность. Так как
нейтральный элемент группы e
принадлежит H, то для любого
элемента a из G и, следовательно,
.
2)
Симмметричность. Из следует существование
в H такого элемента h, что
. Отсюда
получаем, что
. Так как H - подгруппа,
то h-1 принадлежит H
и, следовательно,
.
3)
Транзитивность. Пусть и
. Это означает, что в H
существуют такие элементы h1
и h2, что a = b ° h1
и b = c ° h2. Отсюда
получаем, что a = b ° h2 ° h1.
Так как H - подгруппа, то
произведение h2 ° h1
принадлежит H и,
следовательно, aєc .
Известно,
что любое отношение
эквивалентности, заданное на
некотором множестве, определяет
разбиение этого множества на
непересекающиеся классы
эквивалентных элементов.
Следовательно, и отношение ,
заданное на множестве G с
помощью подгруппы H,
определяет разбиение множества G
на классы эквивалентности. Эти
классы называют левыми смежными
классами группы G
по подгруппе H, а
само разбиение называют левосторонним
разложением G группы
по подгруппе H.
Левый
смежный класс группы G по
подгруппе H,
содержащий элемент a, обозначим aH.
Из определения отношения следует,
что каждый элемент смежного класса aH
имеет вид a ° h, где
.
Заметим,
что одним из левых смежных классов
является само множество H. Этим
классом служит класс eH,
порожденный нейтральным элементом e.
Пример 1.1. Рассмотрим группу поворотов на углы кратные p/ 6 радианам G = <{R0, R1, R2, R3, R4, R5}; °>, где Ri - поворот на i х p / 6 радиан (i = 0, 1, 2, 3, 4, 5), и подгруппу H = <{R0, R3}; °>. Левыми смежными классами группы G по подгруппе H являются:
R0H = {R0, R3}, R1H = {R1, R4}, R3H = {R2, R5}.
Очевидно, .
Пример 1.2. Рассмотрим группу радиус-векторов плоскости относительно операции сложения
и подгруппу радиус-векторов лежащих на оси Oy
Левыми смежными классами группы по подгруппе являются множества
Геометрически (рис. 1.1) каждый из смежных классов (a, b)H представляет собой множество радиус-векторов, концы которых лежат на прямой, параллельной оси Oy и проходящей через точку (a, 0).
Рис. 1.1. Геометрическое представление смежных классов
Пример
1.3. Пусть и
- аддитивная подгруппа целых
чисел кратных 5. Подгруппа
определяет эквивалентность:
то есть
Таким
образом, в один смежный класс
попадают целые числа, которые при
делении на пять дают одинаковые
остатки. Всего получается пять
левых смежных классов (рис. 1.2).
| 0H | ... | -20 | -15 | -10 | -5 | 0 | 5 | 10 | 15 | 20 | ... |
| 1H | ... | -19 | -14 | -9 | -4 | 1 | 6 | 11 | 16 | 21 | ... |
| 2H | ... | -18 | -13 | -8 | -3 | 2 | 7 | 12 | 17 | 22 | ... |
| 3H | ... | -17 | -12 | -7 | -2 | 3 | 8 | 13 | 18 | 23 | ... |
| 4H | ... | -16 | -11 | -6 | -1 | 4 | 9 | 14 | 19 | 24 | ... |
Рис. 1.2. Пять смежных классов
Этот пример показывает, что левостороннее разложение бесконечной группы может иметь конечное число классов.
Пример 1.4. Если G=H , то левостороннее разложение группы G по подгруппе H состоит в точности из одного смежного класса G.
Пример
1.5. Если H = {e}, то
каждый левый смежный класс
левостороннего разложения группы G
по подгруппе H содержит
в точности один элемент группы G,
а отношение эквивалентности
совпадает с обычным равенством.
Смежные классы позволяют доказать теорему Лагранжа, в которой говорится об одном интересном свойстве конечных групп.
Теорема Лагранжа. В каждой конечной группе порядок любой ее подгруппы является делителем порядка группы.
Доказательство.
Пусть G- конечная
группа порядка m, H-
ее подгруппа порядка n.
Рассмотрим левостороннее
разложение группы G по
подгруппе H. Пусть оно
состоит из k смежных классов.
Так как подгруппа H состоит
из n элементов, то и каждый
смежный класс aH также
состоит из n элементов, так как
из ![]() следует
следует
.
Поэтому m = k х n.
При определении левостороннего разложения группы G по подгруппе H мы использовали следующее отношение эквивалентности на множестве G элементов группы:
Если
отношение
заменить на
:
то мы придем к понятию правого смежного класса Ha группы G по подгруппе H, порожденному элементом a, и к правостороннему разложению группы по подгруппе.
Для абелевых групп, очевидно, левостороннее и правостороннее разложения группы G по подгруппе H совпадают.
Пример 1.6. Пусть G- мультипликативная группа невырожденных матриц второго порядка над полем действительных чисел R, а H- подгруппа группы G , состоящая из матриц с определителем равным 1. Множества всех матриц с равными определителями образуют левостороннее (а также и правостороннее) разложение группы G по подгруппе H.
Этот
пример показывает, что и в
некоммутативных группах могут быть
подгруппы по которым левосторонние
разложения совпадают с
правосторонними.
Пример
1.7. Рассмотрим теперь
симметрическую группу третьей
степени S3,
состоящую из подстановок
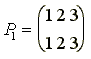
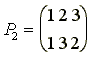
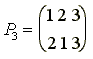
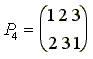
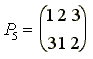
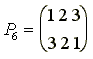
и подгруппу H, состоящую из подстановок P1 и P3.
Левыми смежными классами группы по подгруппе H являются множества:
{P1,
P3}, {P2, P4},
{P5, P6},
а правыми
смежными классами - множества:
{P1,
P3}, {P2, P5},
{P4, P6}.
Пример
показывает, что левостороннее
разложение группы G по
подгруппе H может не
совпадать с правосторонним
разложением по той же подгруппе
H.
Как было показано выше, левый и правый смежные классы одного и того же элемента могут не совпадать (пример 1.7). Однако, особый интерес представляет случай когда эти классы совпадают для любого элемента группы.
Определение 2.1. Подгруппа H называется нормальным делителем группы G или инвариантной подгруппой группы G, если для любого элемента a из G выполняется условие:
aH
= Ha.
Пример
2.1. В любой абелевой группе
каждая ее подгруппа является
нормальным делителем.
Пример
2.2. В мультипликативной
группе невырожденных матриц
второго порядка над полем
действительных чисел подгруппа
матриц с определителем равным 1
является нормальным делителем.
Лемма 2.1. Пусть H - нормальный делитель группы G= <G; °>. Отображение "° ", сопоставляющее двум смежным классам aH и bH третий в соответствии с равенством:
aH
° bH = (a ° b)H,
определяет бинарную алгебраическую операцию на множестве смежных классов группы G по нормальному делителю H.
Доказательство.
Смежный класс, полученный в
результате отображения "° ", не
зависит от выбора представителей
из смежных классов aH и bH (рис.
2.1). Действительно, пусть x aH
и y bH. Это означает, что в H
существуют такие элементы h1
и h2, что x = a h1
и y = b h2.
Поэтому x y = (a h1) (b h2)
= a (h1 b) h2.
Так как (h1 b) bH =
Hb, то в H существует такой
элемент h3, что h1 b
= b h3 и,
следовательно, x y = (a b) (h3 h2).
Так как (h3 h2) H,
то x y (a b)H. Таким
образом, отображение ""
является бинарной алгебраической
операцией на множестве смежных
классов.
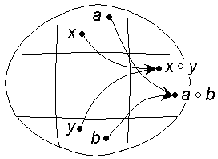
Рис. 2.1. Отображение ""
Теорема 2.1. Множество смежных классов группы по нормальному делителю образует группу относительно операции умножения классов.
Доказательство. Ассоциативность операции умножения классов следует из ассоциативности умножения элементов группы:
(aH bH) cH = ((a b) c)H = (a (b c))H = aH (bH cH).
Единицей служит класс eH. Обратным к классу aH является класс a-1H. Таким образом, все аксиомы группы выполняются.
Определение 2.2. Группа смежных классов группы по нормальному делителю относительно операции умножения классов называется фактор-группой группы по нормальному делителю и обозначается /.
Пример 2.3. Пусть = <Z; +> и = <{5 x x Z}; +> - аддитивная подгруппа целых чисел кратных 5. Фактор-группа / состоит из пяти смежных классов (рис. 2.1).
| + | 0H | 1H | 2H | 3H | 4H |
| 0H | 0H | 1H | 2H | 3H | 4H |
| 1H | 1H | 2H | 3H | 4H | 0H |
| 2H | 2H | 3H | 4H | 0H | 1H |
| 3H | 3H | 4H | 0H | 1H | 2H |
| 4H | 4H | 0H | 1H | 2H | 3H |
Рис. 2.1. Фактор-группа /
Пример 2.4. Пусть - группа радиус-векторов плоскости относительно операции сложения
= <{(x, y) x, y R}; +>,
- подгруппа радиус-векторов, лежащих на оси Oy
= <{(0, y) y R}; +>.
Фактор-группа / геометрически представляется совокупностями радиус-векторов, концы которых лежат на прямых, параллельных оси Oy (рис. 2.2).
Рис. 2.2. Фактор-группа
По сути дела элементами фактор-группы / являются прямые, параллельные оси Oy, а групповая операция над смежными классами является операцией над этими прямыми.
Очевидно, полученная фактор-группа / изоморфна аддитивной группе действительных чисел <R; +>.
Понятие
фактор-группы играет важную роль
при изучении гомоморфизмов групп.
Напомним определение гомоморфизма групп [1].
Определение 3.1. Пусть 1 = <G1; > и 2 = <G2; > - две группы. Гомоморфизмом группы 1 на группу 2 называется сюрьекция :G1 G2 множества G1 на множество G2, сохраняющая групповую операцию:
(a1, b1 G1) (a1 b1) = (a1) (b1).
Определение 3.2. Пусть - гомоморфизм группы 1 на группу 2. Множество всех элементов группы 1, отображающихся в единицу группы 2, называется ядром гомоморфизма и обозначается Ker .
Теорема 3.1. Ядро H = Ker всякого гомоморфизма группы 1 на группу 2 является нормальным делителем группы.
Доказательство. Если a1, b1 Ker , то (a1) = e2 и (b1) = e2. Следовательно, (a1 b1) = (a1) (b1) = e2 e2 = e2, то есть a1 b1 Ker . Кроме того, если a1 Ker , то (a1-1) = (a1) -1 = e2 -1 = e2, то есть a1-1 Ker . Поэтому ядро гомоморфизма Ker образует подгруппу группы 1.
Покажем теперь, что для любого x из G1 выполняется равенство xH = Hx. Если a1 xH, то в H существует элемент h такой, что a1 = x h . Следовательно, (a1) = (x h) = (x) (h) = (x) e2 = (x). Так как 1 - группа, то существует элемент g G1 такой, что a1 = g x. Из (a1) = (g x) = (g) ( x) и (a1) = (x) вытекает, что (g) = e2, и, следовательно, g Ker = H. Поэтому a1 = g x Hx и xH Hx. Аналогично показывается, что Hx xH. Следовательно, xH = Hx и Ker - нормальный делитель группы 1.
Следствие
3.1. Пусть - гомоморфизм группы
1 на группу 2 и H
= Ker - ядро гоморфизма. Два
элемента x и y группы 1
лежат в одном смежном классе группы
1 по нормальному делителю H
тогда и только тогда, когда их
образы при гоморфизме совпадают (x)
= (y).
Рис.
3.1. Гомоморфные группы
Следует из доказательства теоремы 3.1 (рис. 3.1).
Теорема 3.2. Пусть = <G; > - группа и - ее нормальный делитель. Отображение , сопоставляющее каждому элементу x из тот смежный класс xH, которому этот элемент принадлежит, является гомоморфизмом группы на фактор-группу /.
Доказательство. Сюрьективность отображения следует из условия x xH. Если теперь x, y G, то (x y) = (x y)H = xH yH = (x) (y). Таким образом, - гомоморфизм группы на фактор-группу /.
Определение 3.3. Пусть = <G; > - группа и - ее нормальный делитель. Отображение , сопоставляющее каждому элементу x из смежный класс xH, называется каноническим гомоморфизмом группы на фактор-группу /.
Очевидно, что ядром канонического гомоморфизма группы на фактор-группу / является нормальный делитель .
Отсюда, в частности, следует, что нормальные делители и только они служат ядрами гомоморфизмов этой группы.
Важным в теории групп является вопрос, на какие вообще группы может гомоморфно отображаться данная группа . Оказывается все группы, на которые данная группа может отображаться, по существу исчерпываются фактор-группами этой группы, а все гомоморфизмы группы - ее каноническими гомоморфизмами. Точнее справедлива следующая теорема.
Теорема о гомоморфизмах групп. Пусть - гомоморфизм группы 1 на группу 2 и H = Ker - ядро этого гоморфизма. Тогда группа 2 изоморфна фактор-группе 1 / , причем существует такой изоморфизм :1 / 2, что результат последовательного выполнения канонического гомоморфизма :1 1 / и изоморфизма совпадает с гомоморфизмом .
Доказательство. Рассмотрим отображение фактор-группы 1 / на группу 2, ставящее в соответствие каждому смежному классу gH элемент (g), в который при гомоморфизме отображаются элементы класса gH (рис. 3.2).
Рис. 3.2. Отображение группы 1 / на группу 2
Очевидно, отображение является взаимно-однозначным. Покажем, что является изоморфизмом группы 1 / на группу 2. Действительно, пусть pH и gH - произвольные элементы фактор-группы 1 / . Тогда (pH gH) = ((p g)H) = (p g) = (p) (g) = (pH) (gH). Поэтому - является изоморфизмом группы 1 / на группу 2. Рассмотрим теперь композицию отображений , где - канонический гомоморфизм группы 1 на фактор-группу 1 / . Докажем, что = . Пусть g - произвольный элемент группы 1. Тогда (g) = (gH) = (g) и, следовательно, = . Таким образом, теорема доказана.
Теорема о гомоморфизмах показывает, что все группы, на которые может гомоморфно отображаться группа , фактически исчерпываются ее фактор-группами, а все гомоморфизмы группы исчерпываются каноническими гомоморфизмами на ее фактор-группы.
Подробнее
познакомиться с затронутыми в
статье понятиями можно в книгах [2,
3].
1.Емельченков Е.П.,Кристалинский Р.Е. Группы и симметрии. Математическая морфология.
Том 1. Выпуск 1. - Смоленск: Изд-во СГМА. 1996. С. 3-28.
2. Курош А. Г., Теория групп. - М.: Наука, 1967.
3.Калужнин
Л.А. Введение в общую алгебру. - М.:
Наука, 1973.
Кафедра вычислительной техники
Смоленский государственный педагогический институт им. К. Маркса
Поступила в редакцию 5.06.97.