ИЗБРАННЫЕ
ГЛАВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
УДК 517.927.25 + 517.98
Спецкурс
ОСНОВЫ СПЕКТРАЛЬНОЙ ТЕОРИИ НЕСАМОСОПРЯЖЕНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ
ОПЕРАТОРОВ
© 1997.
В. Д. Будаев
Данная
работа задумана как спецкурс по
спектральной теории
несамосопряженных обыкновенных
дифференциальных операторов,
публикация которого
предполагается в нескольких
номерах журнала. Рассчитан
спецкурс на аспирантов
специальности “дифференциальные
уравнения” и студентов старших
курсов, однако он может быть
интересен и полезен достаточно
широкому кругу читателей
(математиков, физиков, биологов и
т.д.) - специалистам во всех тех
областях науки, в которых возникают
спектральные задачи.
ВВЕДЕНИЕ
Изучение любого реального процесса или явления на языке математики связано с рассмотрением некоторых переменных величин. В роли переменных величин могут выступать, например, координаты движущегося объекта и его скорость; температура тех или иных участков тела; сила переменного тока и его напряжение; вязкость движущейся жидкости и площадь поперечного сечения проводника и т.д. Естественно, изучение любой переменной величины следует начать с вопроса о том, как именно она меняется (быстро или медленно, плавно или скачками), т.е. с вопроса о скорости изменения этой величины. С точки зрения математики, скорость изменения переменной величины есть ее производная. Таким образом, математическое описание того или иного процесса или явления заключается в установлении конкретного вида зависимости между задействованными в этом процессе переменными величинами и их производными. Иными словами, математическая модель процесса или явления всегда связана с тем или иным дифференциальным уравнением, т.е. уравнением, содержащим некоторые переменные величины и их производные.
Рассмотрим теперь одну конкретную физическую задачу - задачу о распределении тепла - которая приведет нас к необходимости изучения проблем, составляющих основу спектральной теории.
Для
простоты будем рассматривать
одномерный случай, т.е. процесс
распределения тепла в тонком
стержне. Один конец стержня
поместим в точку 0 на оси OX, а другой
- в точку 1 (таким образом, длину
стержня для удобства будем считать
единичной). Температуру стержня в
точке x (где 0 x 1) в момент времени t
обозначим через u(x, t). Из физики
известно, что функция u(x, t)
удовлетворяет следующему
дифференциальному уравнению в
частных производных (см., например,
[1]):
(1)
где a2 - величина, характеризующая материал, из которого изготовлен стержень (его теплоемкость, теплопроводность, плотность; в частности, если стержень однороден, то a2 = const). Функция f(x, t) характеризует внешнее воздействие на стержень (интенсивность нагревания или охлаждения). Будем считать для простоты, что a2 = const, f(x, t) 0.
Уравнение
(1), как и практически все
дифференциальные уравнения, имеет
бесконечно много решений. С
практической точки зрения, нам
необходимо выделить одно
конкретное интересующее нас
решение, удовлетворяющее некоторым
дополнительным условиям. В
качестве таких дополнительных
условий, позволяющих выделить из
всей совокупности решений одно,
обычно используют начальное
условие и краевые условия.
Начальное условие
(2) u(x, 0) = j(x)
означает,
что в начальный момент времени (т.е.
при t = 0) распределение температуры
известно и задается некоторой
функцией j(x). Краевые
условия
(3) u(0, t) = 0, u(1, t) = 0
означают,
что на концах стержня
поддерживается постоянная
температура. Тот факт, что она равна
именно нулю, несущественен, т.к. ее
всегда можно “обнулить” простой
заменой переменных
(останавливаться на этом моменте мы
сейчас не будем). Ясно, что условия
(2) и (3) должны быть согласованы, а
именно,
j(0) =j
(1) = 0.
Итак,
требуется найти функцию u(x, t),
удовлетворяющую уравнению (1),
начальному условию (2) и краевым
условиям (3). Для решения этой задачи
применим метод разделения
переменных (метод Фурье). Будем
искать решение уравнения (1) в виде
произведения двух функций, одна из
которых зависит только от x, а
другая - только от t : u(x, t) = X(x) T(t).
Тогда уравнение (1) примет вид
Деля обе
части полученного равенства на (случай,
когда X(x) или T(t) могут обратиться в
ноль, рассматривать сейчас не
будем), получим
Левая
часть зависит только от t (и не
зависит от x), правая часть зависит
только от x (и не зависит от t).
Следовательно, обе части не зависят
ни от x, ни от t, т.е. являются
константой, которую мы обозначим
через (-l). Итак,
.
Таким
образом, уравнение (1) распалось на
два уравнения - одно для функции T(t),
другое - для функции X(x):
(4)
(5) .
Уравнение
(4) - линейное однородное
дифференциальное уравнение
первого порядка. Его общее решение
имеет вид
(6)
где С - произвольная постоянная.
Уравнение
(5) - линейное однородное
дифференциальное уравнение
второго порядка. Его общее решение
выглядит по-разному в зависимости
от знака числа :
(7а)
при
,
(7б)
при
,
(7в)
при
,
где А и В - произвольные константы.
Пока мы
требовали только, чтобы функция u(x,
t) = X(x) T(t) являлась решением
уравнения (1). Попробуем теперь
добиться, чтобы она удовлетворяла
также краевым условиям (3):
u(0,
t) = X(0) T(t) = 0,
u(1,
t) = X(1) T(t) = 0.
Случай,
когда T(t) ? 0, неинтересен,
поскольку в этом случае u(x, t) ? 0, а нас, естественно,
интересуют решения, отличные от
тождественного нуля. Поэтому
(8) X(0) = 0, X(1) = 0.
Итак,
функция X(x) должна не только
удовлетворять уравнению (5), но и
краевым условиям (8). Представим
полученные нами решения (7а) - (7в) в
условия (8):
а)
при
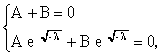
б)
при
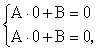
в)
при
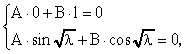
= 0.
Последнее равенство возможно либо
при А = 0 (но тогда снова А = В = 0 и Х(х)
0), либо при
sin = 0,
т.е. при
где n - целое число.
Таким
образом, уравнение (5) с краевыми
условиями (8) имеет ненулевые
решения только при значениях ,
равных и эти решения равны
,
где А - произвольная константа. При n
= 0 снова получаем
, а значения
нет
смысла рассматривать отдельно,
поскольку в выражении для
фигурирует
.
Итак,
окончательно, краевая задача (5) , (8)
имеет ненулевые решения ,
отвечающие значениям
где
. Значения
при
которых краевая задача имеет
ненулевые решения, называются собственными
значениями этой задачи, а
отвечающие им решения
- собственными
функциями этой задачи.
Вернемся
теперь к исходной задаче (1) - (3). При
каждом натуральном n получаем
функцию
(9)
удовлетворяющую
уравнению (1) и краевым условиям (3).
Константа в формуле (9) формально
равна произведению константы А и
константы С из формулы (6). Индекс
“n” у константы
мы поставили,
чтобы подчеркнуть тот факт, что
каждая из функций
отвечает
конкретному значению n.
Каждая из
функций (где
), вообще говоря, не обязана
удовлетворять начальному условию
(2). Однако заметим, что любая
функция вида
(10)
формально
удовлетворяют уравнению (1) и
краевому условию (3) (поскольку
каждое слагаемое является решением
уравнения (1) и удовлетворяет
условию (3)). Подберем коэффициенты в
формуле (10) так, чтобы удовлетворить
начальному условию (2). Подставив (10)
в (2), получим
(11)
Мы,
наконец, подошли к основному
моменту наших рассуждений.
Равенство (11) означает, что функцию (задающую
начальное условие) следует
разложить в ряд по собственным
функциям краевой задачи (5), (8), т.е. в
ряд по системе синусов
Из теории
рядов Фурье хорошо известно, что
такая система синусов является
полной ортогональной системой
функций на отрезке [0, 1], и любую
непрерывно-дифференцируемую (или
даже кусочно
непрерывно-дифференцируемую) на [0,
1] функцию
,
удовлетворяющую условию (0) = (1) = 0,
можно разложить в ряд по этой
системе синусов, равномерно
сходящийся на [0, 1] к функции
.
Коэффициенты разложения находятся
однозначно по формулам
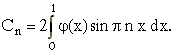
в формулу (10),
получим функцию u(x, t) (в виде ряда),
формально удовлетворяющую как
уравнению (1), так и условиям (2), (3).
Строго
говоря, нам следовало бы убедиться
в сходимости ряда (10) при в
возможности почленного
дифференцирования этого ряда и
сходимости соответствующих рядов
для
и
(без этого мы не можем быть
уверены, что ряд (10) действительно
дает решение исходной задачи).
Однако эти вопросы выходят за рамки
нашей темы, и мы не будем их
рассматривать. Для нас сейчас
важнее другое: решение задачи (1), (2),
(3) фактически свелось к нахождению
собственных значений и собственных
функций задачи (5), (8) и к возможности
разложения заданной функции j(x) в ряд по
собственным функциям. Именно этими
вопросами и занимается
спектральная теория
дифференциальных операторов.
В данной конкретной задаче мы пришли к достаточно простой ситуации: в качестве системы собственных функций у нас возникла хорошо изученная система синусов, в ряд по которой можно разложить любую “хорошую” функцию. К сожалению, далеко не всегда ситуация складывается так удачно.
В качестве
примера, иллюстрирующего возможные
трудности, рассмотрим снова
уравнение теплопроводности (1) с
начальным условием (2) и краевыми
условиями
(3')
Первое из условий (3') означает, что температура на одном из концов стержня поддерживается постоянной, а второе условие означает равенство тепловых потоков на концах стержня: сколько тепла “приходит” через один из концов стержня, столько же “уходит” через другой конец. Отметим, что именно такая задача возникла в физике в 70-х годах нашего века в связи с изучением процессов, происходящих в плазме.
Повторяя
проведенные выше рассуждения,
получим для функции X(x) снова
уравнение (5) и краевые условия
(8')
Легко
убедиться, что при < 0 ненулевых
решений нет. При = 0 получим решение
X(x) = x. При > 0 общее решение
уравнения имеет вид , и при
подстановке в краевые условия
получим
Из второго
уравнения увидим, что либо (и
тогда X(x) ? 0), либо
,
т.е.
Итак,
собственные значения данной задачи
есть (где nI N), а отвечающие
им собственные функции -
Как видим,
собственные значения в данном
случае расположены в два раза
“реже”, чем в первом примере.
Система собственных функций
представляет собой подмножество
рассмотренной выше системы синусов
(с добавлением функции ). Интуитивно
ясно, что собственных функций в
данной ситуации недостаточно,
чтобы разложить произвольную
“хорошую” функцию j(x)
в ряд по этим функциям. Возникает
необходимость пополнить систему
собственных функций некоторым
дополнительным набором функций.
Назовем
функцию присоединенной
функцией, отвечающей собственной
функции
и собственному
значению
, если
удовлетворяет на (0, 1) уравнению
(12)
и на концах интервала удовлетворяет краевым условиям (8').
Нетрудно
проверить, что в нашем примере в
качестве присоединенных функций
можно брать любые функции вида
где -
произвольные константы. Полученная
нами система собственных и
присоединенных функций
(13) 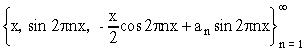
впервые
была исследована лишь в середине
70-х годов в работе Н.И.Ионкина [2].
Оказалось, что свойства этой
системы зависят от выбора констант . Если
последовательность {
} ограничена (и, в
частности, если все
= 0), то система (13)
обладает свойствами, во многом
аналогичными свойствам системы
синусов
:
любая достаточно “хорошая”
функция j(x) может быть
разложена в ряд по этой системе.
Если же последовательность {
}
неограниченна, то система (13) таким
свойством не обладает.
Внимательный
читатель, очевидно, заметил, что
присоединенные функции введены
нами пока чисто формально, в связи с
необходимостью пополнить систему
собственных функций. Однако, в
конечном итоге, с помощью
присоединенных функций можно
получить решение исходной задачи
(1), (2), (3') в виде ряда, аналогичного
ряду (10) для задачи (1), (2), (3). В самом
деле, пусть нам удалось разложить
функцию j(x) в ряд по
системе собственных и
присоединенных функций :
(14)
Будем
искать решение задачи (1), (2), (3') в
виде ряда
(15)
где n
- некоторые константы. Ясно, что при
t = 0 ряд (15) совпадает с рядом (14), т.е.
u(x, 0) = (x). Таким образом, функция u(x, t)
удовлетворяет начальному условию
(2). Выполнение краевых условий (3')
также очевидно, поскольку каждая из
функций Xn(x) и удовлетворяет краевым
условиям (8'). Осталось убедиться,
что функция u(x, t) формально
удовлетворяет уравнению (1) при
надлежащем выборе n (на
вопросах сходимости ряда (15) и
возможности его почленного
дифференцирования мы снова не
будем останавливаться). Для этого
найдем
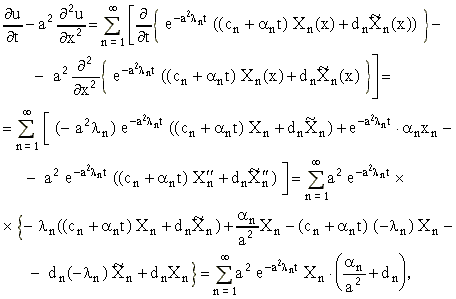
где в предпоследнем равенстве мы воспользовались уравнениями (5) и (12).
Полагая получим, что
т.е. функция (15) удовлетворяет
уравнению (1) и, следовательно,
является решением рассматриваемой
задачи.
Подытожим основные моменты наших рассуждений.
1. Решение краевых задач для уравнений в частных производных (которыми описывается подавляющее большинство физических, химических, биологических и т.д. процессов) методом Фурье приводит к проблеме о возможности разложения данной функции (x) в ряд по собственным функциям некоторой краевой задачи для обыкновенного дифференциального уравнения. Эта проблема и составляет основу спектральной теории дифференциальных операторов.
2. Свойства системы собственных функций существенно зависят как от конкретного вида краевых условий, так и от коэффициентов уравнения (что мы увидим в дальнейшем).
3. В ситуациях, когда система собственных функций неполна (определение полноты будет дано в главе 1), ее приходится пополнять так называемыми присоединенными функциями (такие ситуации, как мы увидим впоследствии, возникают для так называемых несамосопряженных краевых задач). Свойства полученной при этом системы собственных и присоединенных функций (в дальнейшем, для краткости - системы СПФ) существенно зависят от конкретного способа построения присоединенных функций (которые строятся неоднозначно).
Обратим также внимание на следующие моменты. Мы говорили о равномерной сходимости возникающих рядов. Однако на практике часто бывает достаточно более слабых понятий сходимости (особенно часто используется так называемая “сходимость в среднем”). Кроме того, исследовать сходимость ряда для каждой конкретной функции (x) заведомо нецелесообразно. Напрашивается поставить вопрос иначе: можно ли любую функцию из некоторого класса функций (из некоторого функционального пространства) разложить в ряд по системе собственных и присоединенных функций (СПФ) данной краевой задачи (или даже любой краевой задачи, удовлетворяющей некоторым требованиям), сходящийся в том или ином, заранее оговоренном смысле? При утвердительном ответе на этот вопрос говорят, что система СПФ данной краевой задачи образует базис рассматриваемого функционального пространства.
Таким образом, основной круг проблем спектральной теории заключается в следующем: изучение условий, при которых система СПФ краевой задачи для дифференциального уравнения образует базис в том или ином функциональном пространстве.
В связи с этим напрашивается следующая структура нашего спецкурса.
В главе 1 будут изложены некоторые вопросы функционального анализа. Мы рассмотрим некоторые функциональные пространства, введем понятие базиса пространства, а также тесно связанные с ним понятия полноты, замкнутости, минимальности, безусловного базиса, базиса Рисса; обсудим вопросы о разложении функций данного пространства в ортогональные и биортогональные ряды.
В главе 2 мы рассмотрим основные понятия классической теории линейных дифференциальных операторов, выделим класс краевых условий, обеспечивающих базисность (и даже базисность Рисса) систем СПФ, а также поговорим о сути нового подхода к спектральной теории дифференциальных операторов, предложенного около 20 лет назад В.А.Ильиным (см., например, работы 3-6), учеником которого имеет честь быть автор.
В главах 3-4
будут изложены основные
результаты, полученные в работах
как самого В.А.Ильина, так и
некоторых его учеников (в том числе
и автора спецкурса), благодаря
которым на сегодняшний день можно
утверждать, что основы
спектральной теории, ее фундамент,
практически уже построен.
ЛИТЕРАТУРА
1. Тихонов А. Н., Самарский А. А. Уравнения математической физики. - М. :Наука, 1977. - 736 с.
2. Ионкин Н. И. //Дифференциальные уравнения. - 1977. - Т.13. - №2. -С.294-304.
3. Ильин В. А. //Дифференциальные уравнения. - 1980. - Т.16. - №5. - С.771-794.
4. Ильин В. А. //Дифференциальные уравнения. - 1980. - Т.16. - № 6. - С.980-1009.
5. Ильин В.А. // Доклады АН СССР. -1983. - Т.273. - № 4. - С.789-793.
6. Ильин В.А.
Спектральная теория
дифференциальных операторов. - М.
:Наука, 1991. - 368 с.
Исследование выполнено при поддержке Российского фонда фундаментальных исследований
(Проект
РФФИ №96-01-00181).
Кафедра математического анализа
Смоленского государственного педагогического института им. К. Маркса
Поступила
в редакцию 26.01.97.