и при переменных во времени деформациях (обусловленных пульирующим характером движения крови в сосуде) отставание деформации мембраны от напряжения в ней определяется фазовым углом [4],
БИОФИЗИЧЕСКАЯ
МОРФОЛОГИЯ
УДК
611.13/.16:577.3:53.082.1
АНАЛИЗ УСИЛИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ
МЕДИИ
СТЕНКИ КРОВЕНОСНОГО СОСУДА ПРИ
ИЗМЕНЕНИИ ЕГО ТОНИЧЕСКОГО
СОСТОЯНИЯ
© 1997 г. М.
М. Махнач
На основе
литературных данных о морфологии
стенки кровеносного сосуда
мышечного типа выполнен анализ
распределения усилий в элементах
медии и вызываемых этими усилиями
перемещений.. При анализе введено
понятие "квазистатического
состояния" стенки сосуда,
позволяющее исключить влияние на
процессы деформации даламберовых
сил инерции и рассматривать эти
процессы при равных значениях
давления крови внутри сосуда. В
результате анализа установлено,
что в моменты "квазистатического
состояния" сокращение
миоцитарных волокон вызывает
увеличение внутреннего и
уменьшение наружного диаметра
кровеносного сосуда.
Наличие обширного экспериментального материала, позволяющего описывать стенку кровеносного сосуда как многослойную оболочку было отмечено уже в 1971 году [1]. При таком описании становится возможным разделить силы, которые вызывают деформацию стенки сосуда мышечного типа, на внешние и внутренние. Внешние силы - это статическое и динамическое давления крови внутри сосуда, реактивные силы со стороны окружающей кровеносный сосуд биологической ткани, внутренние силы - усилия сокращения миоцитарных волокон, расположенных в среднем слое (media) стенки кровеносного сосуда. Используемый здесь термин "внутренние силы" подразумевает только усилия возникающие от сокращения миоцитарных волокон и не распространяется на внутренние напряжения, возникающие в элементах стенки медии.
Целью данной работы является анализ биомеханики элементов медии и качественное описание деформаций стенки сосуда от усилий ызываемых сокращением миоцитарных волокон. Для проведения такого анализа в качестве исходных приняты следующие данные:
1. Media имеет композитную структуру и представляет собой оболочку, состоящую из нескольких (до 60) коаксиальных крупноокончатых мембран (membranae elasticae fenestratae), соединенных между собой гладкомыщечными волокнами, оплетенными в свою очередь тончайшими волокнами коллагена. Полость между мембранами заполнена различными тканями губчатой структуры и жидкостью. [2,3,4,5].
2. Гладкомышечные клетки и волокна располагаются в среднем слое стенки сосуда продольно и наклонно (угол между направлением оси миоцитов и продольной осью сосуда составляет 30о-50о). В мелких, периферийных сосудах их направление ближе к кольцевому. [2, 3, 5, 6].
и при
переменных во времени деформациях
(обусловленных пульирующим
характером движения крови в сосуде)
отставание деформации мембраны от
напряжения в ней определяется
фазовым углом [4],
где p -разностное давление,
действующее на мембрану, ri -
радиус срединной линии стенки
мембраны, hi- толщина стенки
мембраны,
h - коэффициент вязкости жидкой фазы материала мембраны,
w - угловая частота периодического процесса пульсаций давления крови внутри сосуда,
Един - динамический модуль Юнга. Един>Е и зависит от частоты .
4. Сокращение и расслабление миоцитарных волокон в стенке кровеносного сосуда происходит очень медленно, настолько медленно, что для одного цикла сокращения сердечной мышцы деформацию стенки сосуда, вызываемую действием внутренних сил, можно считать постоянной. Способность миоцитарных волокон к сокращению достигает 25%. [2,4,5].
5. Наружная эластическая мембрана (externa elastica lamina) также имеет окончатое строение, входит в структуру медии и имеет многочисленные точки крепления к ней толстых эластиновых и коллагеновых волокон адвентиции стенки сосуда. Адвентиция при этом рассматривается как жесткий по отношению к медии каркас из эластино-коллагеновых элементов, служащий опорой для миоцитарных волокон медии. [2,4,9].
6.
Биомеханические процессы в медии
при изменении тонического
состояния стенки сосуда
рассматриваются при постоянных
внешних нагрузках и
квазистатическом состоянии стенки
сосуда.
Рис.1
Схема
крепления миоцитарного волокна АВ
к эластическим мембранам mi и
mk медии стенки
кровеносного сосуда и приложенных
к ним усилий Ti и Tk.
На рис.1 приведена схема крепления миоцитарного волокна к эластическим мембранам медии mi и mk (не обязательно соседним k - i ?1) в общем случае косого расположения волокон под углом по отношению к продольной оси сосуда. При косом расположении структурного элемента медии, содержащего миоцитарные волокна, угол его наклона к продольной оси сосуда определяется следующими парметрами:
разностью радиусов внутренних эластических мембран ri и rk, к которым крепится структурный элемент;
некоторой базовой длиной dl - расстоянием между точками крепления структурного элемента по продольной оси сосуда;
координатами
j, выражающими
угловое смещение между точками
крепления концов структурного
элемента к эластическим мембранам.
При j=j i - j k = 0 получаем
случай продольного расположения
миоцитарного волокна, а при dl = 0
имеем поперечное (циркулярное)
расположение миоцитарного волокна.
В общем случае эту зависимость
можно представить в виде функции =
f(dl, ri, rk, j).
Для анализа пределов изменения
угла при некоторых постоянных
значениях dl, ri и rk
рассмотрим схему, изображенную на
рисунке 2.
Рис.
2.
Проекция
"оси" миоцитарного волокна АВ
на плоскость перпендикулярную
продольной оси сосуда
Отрезок
АВ представляет собой проекцию
"оси" миоцитарного волокна на
плоскость перпендикулярную
продольной оси сосуда. Его длина a
связана с радиусами мембран ri
и rk соотношеним
(по теореме косинусов).
При j = 0 аmin = rk
- ri . Наибольшее значение
длина отрезка А`В принимает , когда а
= а' и является касательной к
поверхности мембраны меньшего
радиуса. В этом случае rk2
- ri2 = (a')2 , amax
=.
Исходя из
значений аmin и аmax
а значение
угла g будет
находиться в интервале
Сокращение миоцитарного волокна в точках А и В его прикрепления к мембранам вызывает на них воздействие с усилиями
Тi = Тk
(См.рис.1). При разложении этих
усилий на осевые, радиальные и
тангенциальные составляющие
получаем Тix = Тkx ,
поскольку
Тi cos g = Tk cos g.
Исходя из
условия равновесия сил Tiri
= Tk rk , или
Поскольку rk
> ri , то Тit > Тkt . Значения
радиальной и тангенциальной
составляющих усилия Тi
связаны соотношением
(Тi
sin g)2 = Тi2
+ Tir2,
а усилия Тk
соотношением
(Tksin g)2 = Тk2 + Tkr2,
т.е.
.
Но так как Тit> Tkt , то и Тkr2 - Tir2>0, т.е. Тkr > Tir .
При рассмотрении стенки кровеносного сосуда как многослойной оболочки в качественном описании зависимости ее деформации от усилий, вызываемых сокращением миоцитарных волокон и пульсовым изменением давления крови внутри сосуда в деформации стенки сосуда следует выделять следующие радиальные перемещения (см. рис.3,4):
перемещение
внутренней эластической мембраны wв
; перемещение наружной
эластической мембраны wе;
перемещение наружной поверхности
кровеносного сосуда w. Перемещения wв
, wе , w определяются суммарным
действием на них сил в радиальном
направлении. Действие на mi
мембрану радиальных составляющих Тir
усилий Тi , возникающих при
сокращении множества
прикрепленных к мембране
миоцитарных волокон, можно
представить как равномерно
распределенную по поверхности
мембраны радиальную нагрузку qi.
Рис.
3
Cхема
перемещений внутренней wв
и наружной we эластических
мембран и наружной поверхности
сосуда w при сокращении миоцитарных
волокон медии. Давление крови
внутри сосуда неизменно (pвj =
Const)
Согласно одному из принципов механики - принципу Даламбера - система сил, приложенных к каждой из точек рассматриваемой механической системы, будет находиться в равновесии, если к каждой из точек системы, кроме фактически действующих на нее внешних и внутренних сил, приложены соответствующие даламберовы силы инерции. Для k-й точки механической системы
Fke + Fki + Fkи = 0. [10]. Даламберова сила инерции Fkи = mk ak . Fke - внешняя сила, приложенная к точке системы, Fki - внутренняя сила, приложенная к точке системы, mk - масса точки ,
- ускорение
перемещения wk точки в
пространстве.
Рис.4.
Схема перемещений внутренней wв и наружной we эластических мембран и наружной поверхности сосуда w при изменении (увеличении) давления крови pв внутри сосуда. Натяжение миоцитарных волокон неизменно. Ti = Tk = Const.
Для
мембраны медии как для
механической системы практически
невозможно выделить множество
точек, обладающих какой-то
определенной массой. Для анализа
действия внешних и внутренних сил
на элементы медии удобно ввести
понятие "квазистатического
состояния" стенки кровеносного
сосуда в некоторые моменты времени
tj (j = 1,2,...n), когда скорость
перемещения стенки постоянна
,
а ускорение аk = 0.
Кроме того
в моменты tj давление крови
внутри сосуда имеет одно и то же
значение
рв1
= рв2 = ... = рвn .
Для каждой
мембраны медии условия равновесия
в радиальном направлении в моменты
времени tj будут определяться
условием
.
Поскольку мембраны медии имеют крупноокончатое строение, то давление жидкой фазы медии рm одинаково во всех ее точках и равно давлению жидкой фазы адвентиции рa рассматриваемого участка кровеносного сосуда.
Условие равновесия промежуточной мембраны mi (рис. 5 б)
qik
+ pm - qih - pm = 0
или
qik
- qih = 0
т. е. в квазистатическом состоянии qik = qih и изменение распределенной нагрузки qik` = qih` при дополнительном натяжении миоцитарных волокон первоначально не вызывает перемещения промежуточных мембран.
Деформацию
промежуточной мембраны mi в j-й
момент времени можно положить
начальной и перемещение мембраны в
этот момент
.
Условие
равновесия для внутренней мембраны
mв (рис.5в)
pв
+ qв - pm = 0 ,
где рв - давление крови внутри сосуда. При изменении внутренних усилий Тi (дополнительное сокращение миоцитарных волокон) и изменении (приращении) значения qв на величину Dqв дополнительное перемещение внутренней мембраны будет
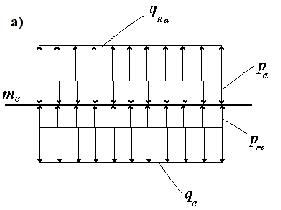
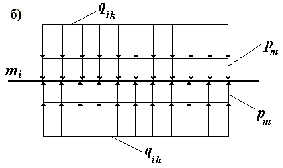
Рис.5
Схемы приложения нагрузок к внутренней mв , промежуточной mi и наружной me эластическим мембранам медии при "квазистатическом состоянии" стенки кровеносного сосуда.
Изменение
внутренних усилий и перемещение
внутренней эластической мембраны
вызывает увеличение давления в
жидкой фазе медии, что в свою
очередь нарушает равновесие
промежуточных мембран и вызывает
их дополнительные перемещения Dwi и переход к
новому квазистатическому
состоянию с параметрами
qi`=
qi +Dqi, wi`=
wi +Dwi, pm`=
pm +Dpm .
При воздействии равномерно распределенной радиальной нагрузки qe на наружную эластическую мембрану в местах крепления к ней эластино-коллагеновых элементов адвентиции возникают радиальные реактивные силы связи, которые на рис.5а изображены как нагрузка qRa. Условие равновесия для наружной мембраны будет qRa + pm - pa - qe = 0, где
qe - равномерно распределенная нагрузка от радиальных усилий миоцитарных волокон, прикрепленных к наружной эластической мембране,
qRa - равномерно распределенная нагрузка от реактивных сил в местах крепления к наружной эластической мембране эластино-коллагеновых элементов адвентиции.
При равенстве давлений жидких фаз медии рm и адвентиции рa,
qRa = qe . Начальное перемещение наружной мембраны we = 0.
При
увеличении усилий Тi и
радиальной нагрузки qe на
величину Dqe,
увеличение внутреннего давления
жидкой фазы медии на Dрm
соответственно увеличивается qRa
и qRa + DqRa = qe
+Dqe . Перемещение
наружной эластической мембраны при
этом
.
Но увеличение нагрузки до значения qe` = qe + Dqe вызовет и деформацию эластино-коллагеновых элементов адвентиции и соответствующее этому встречное перемещение наружной эластической мембраны wej``.
В целом
дополнительное перемещение
наружной эластической мембрны
будет wej = wej`- wej``
(рис.3). При неизменном тоническом
состоянии стенки сосуда (рис.4) (qi
= Const) и пульсирующих изменениях
давления крови внутри сосуда pв
= pв (t) нарушение
квазистатического равновесия
внутренней эластической мембраны и
ее перемещения вследствие
деформации будут вызывать почти
синхронные перемещения
промежуточных мембран медии и
деформации стенки сосуда в целом.
Такие перемещения будут отличаться
от описанных лишь тем, что они
вызываются изменеием давления
крови рв .
Выводы
и заключение
Анализ усилий и перемешений, возникающих в элементах стенки кровеносного сосуда при изменении его тонического состояния показывает следующее.
волокон медии элементов стенки сосуда и равными значениями давления крови внутри сосуда pв1 = pвj ....= pвn сокращение миоцитарных вызывает увеличение внутреннего радиуса сосуда (увеличение просвеа) на величину Dwв` одновременное уменьшение его наружного радиуса на величину Dwe`, Dwв`> Dwе`.
2. При неизменном тоническом состоянии миоцитарных волокон медии периодические пульсовые увеличения давления крови внутри сосуда вызывают увеличение как внутреннего (на величину Dwв`` так и наружного (на величину weD``) радиусов сосуда, Dwв`` > Dwe``.
Автор понимает противоречивость вывода об увеличении внутреннего диаметра кровеносного сосуда при сокращении миоцитарных волокон медии традиционным представлениям о механизмах вазоконстрикции и вазодилатации. Однако считает возможным предложить излагаемый аналитический материал в качестве рабочей гипотезы для последующего экспериментального определения поведения гладкомышечных волокон стенки кровеносного сосуда при регуляции кровотока по следующим причинам:
в большинстве исследований нейрогенных и нейрогуморальных механизмов регуляции кровообращения, которые подробно проанализированы и обобщены в [11] рассматриваются лишь входные (возмущения) и выходные (изменения минутного расхода крови и давления) параметры минуя анализ тонического состояния активного элемента стенки сосуда - медии;
существуют
противоречия в результатах
исследований действия препаратов,
вызывающих сужение или расширение
сосудов, при местном нанесении их
на стенки артерий, а также
отсутствуют убедительные
доказательства в пользу миогенной
либо метаболической гипотез
вазомоторики [11].
Литература
1. Регирер С. А. Некоторые вопросы гидродинамики кровообращения. //Гидродинамика кровообращения. Под ред. С. А.Регирера. - М.: Мир, 1971. - 270 с.
2. Пуриня Б. Я., Касьянов В. А. Биомеханика крупных кровеносных сосудов человека. - Рига: Зинатне, 1980. - 260 с.
3. Никулин А. А., Петров В.К. Кровеносные сосуды. -Тула: Приокское книжное издательство, 1981. - 348 с.
4. Каро К. и др. Механика кровообращения.- М.:Мир, 1981. - 624 с.
5. Гистология. Под ред. Елисеева В.Г. и др.- М.: Медицина, 1983. -592с.
6. Пшеничный А.Н. Взаимопреобразование спиральных D- и L-энантоморфов мышц кровеносных сосудов. //Архив АГЭ.-1985. -№ 5. -С.37-43.
7. Феодосьев В.И. Сопротивление материалов -М.:Наука,1970.- 544с.
8. Писаренко Г.С. и др. Сопротивление материалов. -Киев.: Вища школа, 1986.
9. Ванков В.Н. Строение вен. М.:Медицина, 1974. - 207 с.
10.Тарг С. М. Краткий курс теоретической механики.-М.:Наука, 1967.
11.Марков
Х.М. Патофизиология артериальной
гипертонии. - София: Медицина и
физкультура, 1970.
Исследование
выполнено при поддержке
Российского фонда фундаментальных
исследований (Проект РФФИ №96-04-50991).
Смоленский областной институт патологии
Поступила
в редакцию 14. 01. 97.