УДК 51
ПРИМЕНЕНИЕ ЭКСПОНЕНЦИАЛЬНЫХ ПОЛИНОМОВ
ДЛЯ
СТРУКТУРНОГО БИОМЕХАНИЧЕСКОГО
АНАЛИЗА СОСУДИСТОЙ СТЕНКИ
© 1997 г.
Л. Л. Лямец
В данной
статье изложены результаты
биомеханических исследований
сегментов артерий и мочеточника.
Для анализа результатов
исследований применяются
экспоненциальные полиномы.
Полученные математические модели
рассматриваются как отражение
внутренней структуры исследуемых
биологических объектов.
Установлено и доказано
соответствие между
экспоненциальными составляющими
математических моделей и основными
морфологическими структурами
сосудистой стенки и стенки
мочеточника.
Одним из направлений биомеханики является исследование механических свойств мягких биологических тканей, в том числе стенок кровеносных сосудов.
Для изучения механического поведения сосудов совместно с экспериментальными исследованиями необходима разработка математических моделей. В исследовательских работах по биомеханике прослеживается стремление к созданию универсального математического подхода к оценке биомеханических свойств сосудистой стенки (Fung Y. C., 1975; Пуриня Б.А., Касьянов, 1980).
Главной особенностью зависимостей деформация - напряжение для мягких биологических тканей является их существенная нелинейность. Для количественной оценки механических характеристик применялись ка-сательный модуль упругости, секущий модуль упругости и начальный модуль упругости. Использование указанных параметров является следствием применения классической теории упругости. Данный подход не позволяет в полной мере описать сложное механическое поведение материала стенки кровеносных сосудов и в настоящее время имеет лишь историческую ценность.
Более точное описание механических свойств мягких биологических тканей дают аналитические методы. Для описания нелинейных зависимостей применялись степенные законы разных видов (Sharma M.G., Hollis T. M., 1976). Данный способ аппроксимации эффективен и обладает высокой точностью. Существенным недостатком является невозможность истолкования физического смысла размерностей коэффициентов аппроксимации в понятиях теории упругости. Степенной полином не позволяет построить формальную эквивалентную механическую модель материала сосудистой стенки.
Наиболее широкое распространение получили экспоненциальные функции. На правомерность такой аппроксимации указывают имеющиеся сведения об экспоненциальном характере зависимости деформация - на-пряжение для мягких биологических тканей. Известен способ представления напряжения через энтропийный множитель и экспоненциальную функцию энергии деформации (Fung Y.C., 1967). Однако такое математическое представление не позволяет оценить энергетические вклады отдельных морфологических структур и при описании их механических свойств вызывает необходимость проводить механическое или химическое фракционирование.
В данной работе предлагается аппроксимация нелинейных механических характеристик экспоненциальными полиномами. При определенных условиях анализа результатов экспериментов совокупность простых экспоненциальных процессов, полученная в результате аппроксимации, может являться отражением внутренней структурной организации исследуемой биологической ткани и механических свойств основных морфологических структур.
В связи с
вышеизложенными данными была
поставлена задача исследовать
механические свойства кровеносных
сосудов, аппроксимировать
экспериментально полученные
механические характеристики
экспоненциальными полиномами,
определить соответствие между
экспоненциальными составляющими в
математической модели и основными
морфологическими структурами
сосудистой стенки.
МАТЕРИАЛЫ
И МЕТОДЫ ИССЛЕДОВАНИЯ
Материалом для исследования служили сегменты а. basilaris и a. renalis в виде колец шириной 3 мм., вырезанные перпендикулярно продольной оси сосуда, что в меньшей степени нарушает морфологические связи в стенке кровеносного сосуда и соответствует общепринятой методике. Образцы артерий брались при аутопсии у мужчин, погибших от травм, не позднее 12 часов с момента наступления смерти и были исследованы в течении двух часов с момента взятия материала. Весь исследуемый материал был распределен по двум возрастным группам. Первой группе соответствовал возраст 20-30 лет, второй - 40-60 лет. Исследования проводились в возрастном аспекте, поэтому образцы с явно выраженными атеросклеротическими изменениями (фиброзные бляшки, атерокальциноз и т.п.) в указанные возрастные группы не входили. Всего исследовано 168 артерий каждого типа, по 84 в каждой возрастной группе.
Для контрольных исследований, с целью определения механических свойств гладкомышечной ткани, использовались сегменты мочеточника. Исследовались образцы, взятые у лиц из первой возрастной группы. Из каждого образца вырезались два сегмента, находящихся в непосредственной близости. Всего исследовано 15 образцов мочеточника.
Исследования проводились в два этапа. На первом этапе проводились биометрические исследования. На втором этапе проводились биомеханические исследования.
Биометрические исследования проводились с целью определения основных геометрических размеров сегментов кровеносных сосудов из первой и второй возрастных групп в ненапряженном состоянии. Для исследуемых сегментов кровеносных сосудов в результате измерений определялись: толщина стенки h кровеносного сосуда, внутренний диаметр d, наружный диаметр D. Измерения проводились при помощи микрометра с ценой деления 0.01 мм, оснащенного электрическим индикатором.
Биомеханические исследования проводились с целью получения экспериментальных механических характеристик деформация - напряжение и релаксационных характеристик напряжение - время.
Механические характеристики деформация - напряжение для сегментов кровеносных сосудов определялись путем регулируемого последовательного ступенчатого растяжения с регистрацией усилия, возникающего непосредственно после каждого шага растяжения и после полной релаксации образца. Во время экспериментов образцы находились в физиологическом растворе. Исследования проводились при температурных режимах 20оС и 40оС.
Эксперименты осуществлялись при помощи устройства, обеспечивающего ступенчатую деформацию образца, измерение упругого усилия и его графическую регистрацию. Датчик измерения силы был выполнен на механотроне 6МХ2Б. Рабочий диапазон измерения силы составлял от 24.5 мН до 2.45 Н. Относительная погрешность измерений, определенная в результате калибровочных испытаний измерительной установки, на всем диапазоне измерений не превышала 2.5 %.
По результатам эксперимента для каждого образца строились две характеристики деформация - напряжение. Первая характеристика строилась по точкам для максимальных значений напряжения после ступенчатой деформации, а вторая - по точкам для квазиравновесных значений напряжения после механической релаксации образца. Величина шага деформации, равная 0.2 мм, была выбрана с таким расчетом, чтобы экспериментальные графики деформация - напряжение были построены по 12 - 15 экспериментальным точкам.
В первой группе исследовано по 42 образца a. renalis и a. basilaris. Из этого числа 21 сегмент исследовался при температуре 20оС и 21 сегмент - при температуре 40оС. Аналогичное количество сегментов артерий было исследовано во второй возрастной группе. В контрольных экспериментах 15 сегментов мочеточника исследовано при температуре 20оС и 15 сегментов - при температуре 40оС.
Для исследования релаксационных процессов в образцах артерий измерительная установка использовалась в режиме релаксометра. После того, как образец артерии был закреплен в зажимах, ему задавалась начальная ступенчатая деформация, равная 50% от длины в ненапряженном состоянии. Процесс релаксации регистрировался в течение 20 минут.
Аппроксимация нелинейных характеристик деформация e - напряжение T(e) производилась при помощи выражения вида:
(1)
В выражении (1) величина eо соответствует началу участка интерполирования, l = e + 1, а коэффициенты Ap и ap подлежат определению. Вычисление коэффициентов аппроксимации производилось интерполяционным методом, описанным в работе [1].
Аппроксимация
экспериментальных релаксационных
графиков напряжение T(t) - время t
проводилась выражением:
(2)
Для вычисления коэффициентов аппроксимации Ei и ti использовался метод наименьших квадратов. Данный метод подробно описан в работе [2].
Количество
экспоненциальных составляющих и
качество аппроксимации
экспериментальных данных
выражениями (1) и (2) оценивалось
сравнением средней квадратичной
относительной погрешности
аппроксимации с относительной
погрешностью измерения. Средняя
квадратичная погрешность
аппроксимации Ф определялась по
формуле:
(3)
где Ti аппр - численные значения функции согласно аппроксимации;
Ti эксп - экспериментальные значения;
N - количество экспериментальных точек.
Предполагалось, что точность аппроксимации экспериментальных результатов достаточна, если средняя квадратичная погрешность аппроксимации не превышала по величине значение относительной погрешности измерения в эксперименте, то есть 2.5%.
На
заключительном этапе исследования
в каждой возрастной группе для
различных температурных режимов
экспериментов проводилась
статистическая обработка
коэффициентов аппроксимации.
РЕЗУЛЬТАТЫ
ИССЛЕДОВАНИЯ
Результаты биометрических исследований сегментов a. basilaris приведены в таблице 1, сегментов a. renalis - в таблице 2.
Таблица 1
| Возрастная группа | Толщина стенки(мм) | Внутренний диаметр(мм) | Внешний диаметр(мм) |
| 1(20 - 30лет ) | 0.41 |
2.52
|
3.34
|
| 2(40 - 60 лет) | 0.49 |
2.85
|
3.83
|
Таблица 2
| Возрастная группа | Толщина стенки(мм) | Внутренний диаметр(мм) | Внешний диаметр(мм) |
| 1(20 - 30 лет) | 0.64 |
3.01
|
4.23
|
| 2(40 - 6 лет) | 0.76 |
3.32
|
4.87
|
Применение t-критерия Стьюдента позволило для каждого типа артерий установить достоверность различия между одноименными параметрами в первой и второй возрастных группах.
Для сегментов исследованных артерии установлено, что с возрастом толщина стенки, внутренний и внешний диаметр артерий достоверно увеличиваются. Очевидно, что полученные результаты отражают общую закономерность изменения размеров кровеносных сосудов с возрастом при отсутствии ярко выраженных патологических изменений.
Математическая обработка результатов биомеханических исследований позволила установить, что при аппроксимации выражением (1) экспериментальных кривых деформация - напряжение для достижения удовлетворительной точности достаточно использовать сумму трех экспоненциальных составляющих с действительными коэффициентами. При этом средняя относительная погрешность аппроксимации, рассчитанная по формуле (3), не превышает 2.5 %. С помощью статистического критерия соответствия c2 установлено, что закон распределения коэффициентов аппроксимации можно считать нормальным.
Экспериментальные
квазиравновесные графики
деформация - напряжение
аналитически можно представить в
виде:
(4)
(5)
Экспериментальные
зависимости деформация -
напряжение для максимальных
значений напряжения можно
представить в виде:
(6)
(7)
Средние
значения и средние квадратичные
ошибки коэффициентов Ar i, ar i и Am i, am i для
сегментов a. basilaris приведены в
таблицах 3 и 4, для сегментов a. renalis -
в таблицах 6 и 7, для сегментов
мочеточника - в таблице 5. Индексом r
обозначены коэффициенты для
квазиравновесных графиков, а
индексом m - коэффициенты графиков,
построенных по максимальным
значениям напряжения.
Таблица 3
| Коэффициенты | Первая возрастная группа | Вторая возрастная группа | ||
| аппроксимации | 20оС | 40оС | 20оС | 40оС |
| А r 1 | 1379 |
884 |
2360 |
1557 |
| a r 1 | 5.93 |
6.12 |
5.873 |
5.96 |
| A r 2 | 6944 |
9831 |
5264 |
7318 |
| a r 2 | 3.61 |
3.75 |
3.83 |
3.93 |
| A r 3 | 915 |
577 |
1894 |
1306 |
| a r 3 | 3.12 |
3.04 |
2.97 |
2.91 |
Таблица 4
| Коэффициенты | Первая возрастная группа | Вторая возрастная группа | |||
| аппроксимации | 20оС | 40оС | 20оС | 40оС | |
| А m1 | 2432 |
1571 |
3556 |
2419 |
|
| a m1 | 5.82 |
6.18 |
5.79 |
6.09 |
|
| A m 2 | 7853 |
11512 |
5637 |
8236 |
|
| a m 2 | 3.66 |
3.63 |
3.92 |
3.87 |
|
| A m 3 | 114236 |
65287 |
123541 |
80238 |
|
| a m 3 | -1.43 |
-1.17 |
-0.63 |
-0.712 |
|
Таблица
5
| Коэффициенты | Квазиравновесный график | График для максимальных значений | ||
| аппроксимации | 20оС | 40оС | 20оС | 40оС |
| А1 | 34.8 |
18.5 |
76.5 |
40.3 |
| a 1 | 6.51 |
6.83 |
6.67 |
6.71 |
| A 2 | 96.7 |
175.2 |
125.6 |
192.3 |
| a 2 | 3.91 |
3.79 |
4.12 |
4.08 |
| A 3 | 3347 |
1942 |
312761 |
245974 |
| a 3 | 2.86 |
3.02 |
-1.32 |
-1.11 |
Таблица 6
| Коэффициенты | Первая возрастная группа | Вторая возрастная группа | ||
| аппроксимации | 20оС | 40оС | 20оС | 40оС |
| А r 1 | 1792 |
1149 |
2951 |
2014 |
| a r 1 | 5.81 |
5.94 |
6.12 |
5.98 |
| A r 2 | 8721 |
10234 |
9842 |
11974 |
| a r 2 | 3.42 |
3.35 |
3.51 |
3.48 |
| A r 3 | 746 |
487 |
1276 |
978 |
| a r 3 | 3.01 |
3.12 |
3.08 |
2.96 |
Таблица
7
| Коэффициенты | Первая возрастная группа | Вторая возрастная группа | ||
| аппроксимации | 20оС | 40оС | 20оС | 40оС |
| А m1 | 2367 |
1713 |
3861 |
2856 |
| a m1 | 5.97 |
6.05 |
6.03 |
5.88 |
| A m 2 | 9259 |
10521 |
10431 |
12104 |
| a m 2 | 3.54 |
3.68 |
3.62 |
3.61 |
| A m 3 | 38248 |
15037 |
86551 |
47264 |
| a m 3 | -1.32 |
-1.21 |
-0.84 |
-0.76 |
Для установления соответствия между экспоненциальными составляющими в математических моделях (4), (6) и основными морфологическими структурами стенки кровеносных сосудов и мочеточника был проведен анализ изменений вкладов экспоненциальных составляющих под воздействием температуры, с возрастом, до и после релаксации.
Два экспоненциальных процесса можно считать достоверно различными, если получено достоверное различие для предэкспонециальных коэффициентов или для коэффициентов в степени экспонент. Статистический анализ одноименных коэффициентов аппроксимации проведен с использованием t - критерия Стьюдента.
Сопоставление результатов статистического анализа с известными особенностями изменения механического поведения основных морфологических структур при изменении температуры (Вилкс Ю. К., Саулгозис Ю. Ж., Янсон Х. А., 1975), с учетом закономерностей их качественной и количественной трансформации с возрастом ( Годлевска М. А., Крегерс А. Ф., Пуриня Б. А., Слуцкий Л. И., 1978) и степенью выраженности релаксационных процессов (Образцов И. Ф., Адамович И.С., Барер А. С., 1988) позволило сделать следующие выводы:
1. Экспоненциальные составляющие Tr 1(e) и Tm 1(e) в математических моделях (4) и (6) отражают механическую реакцию коллагеносодержащих морфологических структур в стенках исследованных артерий и мочеточ-ника.
2. Экспоненциальные составляющие Tr 2(e) и Tm 2(e) отражают механическую реакцию эластиносодержащих морфологических структур в стенках артерий и мочеточника.
3. Экспоненциальные составляющие Tr 3(e) и Tm 3(e) отражают механическую реакцию гладкомышечного ком-понента сосудистой стенки и мочеточника.
На рисунке 1 показаны графики экспоненциальных составляющих Tr1(e) для сегментов a. basilaris из первой и второй возрастных групп при температурных режимах экспериментов 20оС и 40оС. Графики составляю-щих Tm 1(e), Tr 2(e), Tm 2(e), Tr 3(e) имеют аналогичный характер и отличаются коэффициентами в экспоненциальных функциях. Особый интерес представляют графики составляющих Tm 3(e). Для сегментов исследованных артерий и мочеточника математические выражения для Tm 3(e) имеют в степени экспоненты отрицательный показатель am 3. Характер графика определяется произведением возрастающего энтропийного множителя на убывающую экспоненциальную функцию. На рисунке 2 показаны графики составляющих Tm 3(e) для сегментов a. basilaris. Для сегментов почечной артерии и мочеточника графики имеют аналогичный характер. В мочеточнике данная составляющая является преобладающей.
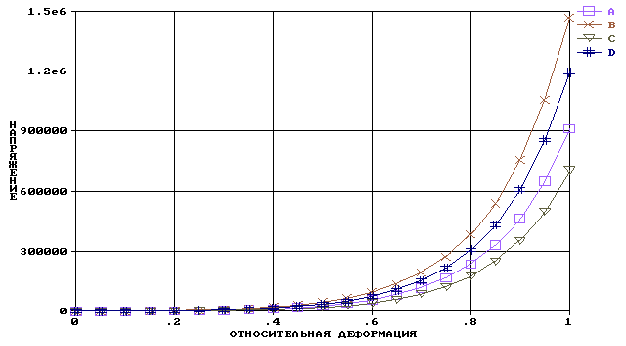
Рис. 1.
Графики составляющих Tr 1(e) для сегментов a.
basilaris.
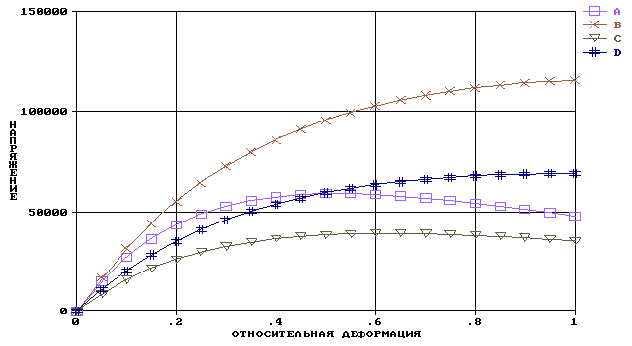
Рис. 2. Графики составляющих Tm3(e) для сегментов a. basilaris
Для идентификации кривых на рисунке введены условные обозначения:
Вклады экспоненциальных составляющих в математических моделях (4) и (6) зависят от возрастного фактора и температуры эксперимента. Это отражается на достоверном изменении предэкспоненциальных коэффициентов. Коэффициенты в степени экспоненциальных составляющих достоверно не изменяются. Для сегментов исследованных артерий и мочеточника данные одноименные коэффициенты имеют близкие по величине численные значения. Они определяют характер нелинейности экспоненциальных составляющих и могут служить качественным признаком основных морфологических структур.
Математическая обработка графиков релаксации напряжения в образцах артерий позволила установить, что во всех случаях для достижения удовлетворительной точности достаточно использовать сумму трех экспоненциальных составляющих с действительными коэффициентами.
Результаты
аппроксимации экспериментальных
графиков релаксации напряжения для
сегментов a. basilaris приведены в
таблице 8, для сегментов a. renalis - в
таблице 9. В таблицах указаны
средние значения и средние
квадратичные ошибки коэффициентов
аппроксимации. Результаты
аппроксимации экспериментальных
релаксационных кривых позволяют
представить данный процесс
математической моделью вида:
(8)
где: .
Принятие решения о соответствии между экспоненциальными составляющими математической модели (8) и основными морфологическими структурами сосудистой стенки было сделано на основании анализа полученных численных значений времени релаксации t, характеризующих скорости изменения напряжения во времени, и зависимости вкладов экспоненциальных составляющих, определяемых предэкспоненциальными коэффициентами, от температуры. Проведенные исследования позволили сделать следующие выводы:
1. Экспоненциальные составляющие T1(t) с коэффициентами E1 и t 1 количественно характеризуют процесс релаксации гладкомышечного компонента сосудистой стенки в a. basilaris и a. renalis. Подтверждением этого может служить наименьшее значение времени релаксации t1 и достоверное уменьшение значения коэффициентов E1 при повышении температуры эксперимента.
2. В отношении экспоненциальных составляющих T2(t) можно утверждать, что они количественно отражают процесс релаксации напряжения коллагеносодержащих морфологических структур в стенках a. basilaris и a. renalis. В пользу данного заключения говорит достоверное уменьшение значений коэффициентов E2 при повышении температуры и численное значение времени релаксации, занимающее промежуточное положение между значениями коэффициентов t 1 и t 3.
3. Экспоненциальные составляющие T3(t) с коэффициентами E3 и t 3 количественно характеризуют релаксацию напряжения эластиносодержащих морфологических структур в стенках a. basilaris и a. renalis. С повышением температуры значения коэффициентов E3 достоверно увеличиваются. Это является следствием изменения механических свойств эластиносодержащих морфологических структур в ответ на повышение температуры.
Коэффициенты t3, характеризующие время релаксации экспоненциальных составляющих T3(t), имеют наибольшие значения по сравнению с коэффициентами t 1 и t 2. Данный факт отражает особенность эластических волокон, выражающуюся в наибольшей длительности процесса релаксации по сравнению с другими морфологическими структурами стенки кровеносных сосудов.
Одноименные коэффициенты t 1, t 2, t 3, рассчитанные для сегментов a. basilaris и a. renalis, имеют близкие по величине значения. Результаты проведенных исследований можно рассматривать как подтверждение качественного соответствия между релаксационными процессами в основных морфологических структурах сосудистой стенки и экспоненциальными составляющими в математической модели (8).
Таблица 8
| Коэффи-циенты | Первая возрастная группа | Вторая возрастная группа | ||
| аппрокси-мации | 20оС | 40оС | 20оС | 40оС |
| E 1 | 385214 |
269353 |
456761 |
337462 |
| t 1 | 2.15 |
1.91 |
3.86 |
3.43 |
| E 2 | 268313 |
192361 |
372568 |
258608 |
| t 2 | 18.7 |
23.6 |
26.8 |
24.3 |
| E 3 | 232172 |
314227 |
167388 |
224309 |
| t 3 | 117.6 |
133 |
123.6 |
131.2 |
Таблица 9
| Коэффициенты | Первая возрастная группа | Вторая возрастная группа | ||
| аппроксимации | 20оС | 40оС | 20Ос | 40оС |
| E 1 | 234648 |
152483 |
315685 |
268407 |
| t 1 | 2.88 |
2.42 |
3.42 |
3.74 |
| E 2 | 308871 |
186779 |
354128 |
261662 |
| t 2 | 28.4 |
21.7 |
31.3 |
27.5 |
| E 3 | 386992 |
435246 |
429338 |
472356 |
| t 3 | 149.2 |
157.8 |
148.5 |
161.6 |
ВЫВОДЫ
1. В результате проведенного исследования разработан метод аналитического представления экспериментальных графиков деформация - напряжение и релаксационных кривых, полученных для сегментов артерий и мочеточника, суммой экспоненциальных процессов.
2. Решена задача практического определения коэффициентов аппроксимации в экспоненциальных полиномах высокого порядка интерполяционным методом и методом наименьших квадратов.
3. Исследование показало, что экспоненциальные полиномы позволяют с высокой точностью аппроксимировать экспериментальные графики.
4. Установлено, что механическая реакция сосудистой стенки на растяжение может быть представлена в виде формальной математической модели как сумма механических реакций коллагеносодержащих, эластиносодержащих, гладкомышечных морфологических структур и аналитически описана суммой трех экспоненциальных составляющих.
5. Установлено соответствие между механической реакцией основных морфологических структур сосудистой стенки и экспоненциальными составляющими математической модели.
6. Описанный метод может быть применен для быстрого анализа составляющих релаксационного процесса в сосудистой стенке.
7. Разработанный метод позволяет анализировать особенности биомеханической реакции основных морфологических структур сосудистой стенки на изменение температуры в физиологических пределах и количественно оценивать изменения возрастного характера.
8. Эксперименты на образцах мочеточника показали, что представление механической реакции на деформацию в виде суммы экспоненциальных процессов может быть применено для биомеханического анализа механического поведения объектов, состоящих, в основном, из гладкомышечной ткани.
9. Предложенный метод может быть использован для структурного биомеханического анализа мягких биологических тканей в норме и патологии на основе единого физико-математического подхода.
ЛИТЕРАТУРА
1. Лямец Л. Л. Аппроксимация нелинейных характеристик экспоненциальными полиномами. // Вторая военно-научная конференция ВА ПВО СВ РФ. Ч. 2. - Смоленск: СВА ПВО СВ РФ, 1995. - С. 146 - 150.
2. Лямец Л.
Л., Методика расчета и программное
обеспечение для вычисления
коэффициентов по методу наименьших
квадратов при аппроксимации
нелинейных характеристик
экспоненциальными полиномами. -
Математическая морфология.- Том 1.
-Выпуск 1.- 1996. - С. 72 - 76.
Смоленская Военная академия ПВО СВ РФ
Поступила в редакцию 20.03.97.