
ПАРАЛЛЕЛЬНЫЕ ВЫЧИСЛЕНИЯ И
МАТЕМАТИЧЕСКАЯ
МОРФОЛОГИЯ
УДК: 519.6:519.725
Изучаются возможности параллельных вычислений на основе методов упаковки графической информации. Достаточно простая модификация последовательных алгоритмов в параллельные достигается за счет их матричного представления. Получены временные оценки различных этапов упаковки при их реализации на многопроцессорных вычислителях.
Введение
Развитие компьютерной графики и совершенствование способов отображения данных на экране монитора привели к созданию целого ряда компьютеров, способных передавать, принимать и воспроизводить сложные графические образы с качеством, приближающимся к телевизионному или полиграфическому. Графика широко используются в таких областях, как образование, компьютерные игры, медицинская биология, компьютерная томография [1]. При этом ,в основном, графические образы занимают большое количество дискового пространства, что приводит к необходимости быстрой и эффективной упаковки информации. Скорость упаковки становится решающим фактором при обработке информации в режиме реального времени, например, в случае записи изображений с видеокамеры в память компьютера. Однако наиболее эффективные (в несколько десятков раз без заметной потери качества) методы упаковки графической информации сводятся к выполнению различных трудоемких операций над матрицей исходного изображения. Это приводит к тому, что требуемые временные характеристики при обработке информации могут обеспечить только параллельные алгоритмы решения задачи для параллельных многопроцессорных ЭВМ [2]. В данной работе анализируется один из наиболее эффективных алгоритмов упаковки изображения, предложенный в конце 80-х годов и получивший название JPEG по имени группы разработчиков - Joint Photographic Experts Group [3,4] . При этом целью являлось изучение возможностей различных схем его вычислений, наилучших с точки зрения параллельной организации. Ожидаемая оценка производительности параллельных вычислений проводилась по следующим параметрам: s - ускорение, e - эффективность, которые определяются следующим образом: s = T(1)/T(p), e = s/p, где T(1) - время реализации алгоритма на одном процессоре, T(p) - время реализации алгоритма на p параллельных процессорах.
В
алгоритме JPEG исходное изображение
представляется двумерной матрицей
размера N*N, элементами которой
являются цвет или яркость пиксела.
Упаковка значений матрицы
выполняется за три этапа,
представленных на рисунке 1.
Рис. 1. Этапы работы алгоритма JPEG
Высокая
эффективность сжатия, которую дает
этот алгоритм, основана на том
факте, что в матрице частотных
коэффициентов, образующейся из
исходной матрицы после дискретного
косинусного преобразования,
низкочастотные компоненты
расположены ближе к левому
верхнему углу, а высокочастотные -
внизу справа. Это важно потому, что
большинство графических образов на
экране компьютера состоит из
низкочастотной информации, так что
высокочастотные компоненты
матрицы можно безболезненно
выбросить. “Выбрасывание”
выполняется путем округления
частотных коэффициентов. После
округления отличные от нуля
значения низкочастотных компонент
остаются, главным образом, в левом
верхнем углу матрицы. Округленная
матрица значений кодируется с
учетом повторов нулей. В результате
графический образ сжимается более
чем на 90% , теряя очень немного в
качестве изображения только на
этапе округления.
Основные свойства дискретного косинусного преобразования, обеспечивающие возможность параллельных вычислений
Основным этапом работы алгоритма является дискретное косинусное преобразование (ДКП), представляющее собой разновидность преобразования Фурье. Оно позволяет переходить от пространственного представления изображения к его спектральному представлению и обратно. Результат ДКП для функции F(x,y), заданной матрицей F на множестве дискретных значений 0<=x<N и 0<=y<N, - это матрица D частотных коэффициентов размера N*N . Схема вычисления коэффициентов матрицы D определяется выражением
(1) 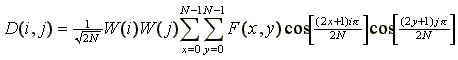
где
(2) ,
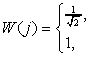
.
Выражение для обратного преобразования матрицы “гармоник”, применяемое при распаковке изображения записывается в виде
(3) 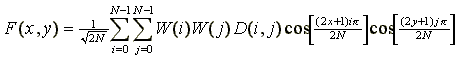
где W(i), W(j) определяются выражениями (2).
Время,
необходимое для вычисления каждого
элемента матрицы ДКП зависит от ее
размера. Так как для вычисления (1)
необходимо два вложенных цикла, то
время вычисления одного элемента
матрицы составляет O(N2).
Время вычисления N*N элементов
всей матрицы изображения на
однопроцессорной ЭВМ составит O(N4).
Согласно [5], степень параллелизма
(число арифметических независимых
операций, которые поэтому могут
выполняться параллельно, т. е.
совместно или одновременно)
преобразования при
непосредственной реализации
формул типа (1) лежит в диапазоне - N ,
поэтому время его реализации на
многопроцессорной ЭВМ даже при
неограниченном числе процессоров
будет не менее O(N3).
Гораздо большими, на наш взгляд, возможностями обладает вариант вычисления коэффициентов ДКП через стандартные операции умножения матриц, широко используемые при распараллеливании в различных областях[5,6,7]. В этом случае схему вычисления частотных коэффициентов матрицы D целесообразно представить в виде умножения матриц в соответствии с отношением
(4)
,
где F -
матрица исходного изображения, - матрица
постоянных коэффициентов
косинусного преобразования
размера N*N, значения элементов
которой вычисляются по формуле
(5) 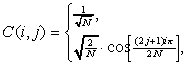
,
- транспонированная
матрица C.
Этот вариант реализации ДКП более привлекателен для распараллеливания еще и потому, что современные архитектуры многопроцессорных вычислителей выполняют стандартные матричные операции умножения и транспонирования. При перемножении двух матриц рамера N*N для вычисления одного элемента результирующей матрицы необходимо выполнить N умножений и N сложений, следовательно время вычисления одного элемента будет равно t1*N, где t1 - время выполнения одной операции типа c=ax+b. Так как число элементов в матрице равно N 2 , а в (4) присутствуют два умножения, то общее время ДКП на одном процессоре будет равно
(6)
.
Оценим время необходимое для перемножения двух матриц размером NxN, если оно происходит на вычислителе с числом процессоров p= R 2, при условии, что N - кратное R и все процессоры могут работать параллельно. B этом случае удобно воспользоваться клеточными методами [8], сводя произведение матриц размера N*N к произведению матриц - клеток размером R*R. В этом случае вычисление произведения X=C*F (X*CT вычисляется аналогично) следует представить через произведение подматриц-клеток меньшей размерности. Разобьем исходные матрицы C, F на подматрицы размера R*R и представим операцию клеточного умножения в форме
(7) 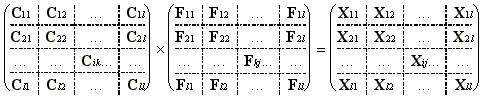
где Cik, Fkj, Xij - подматрицы- клетки размера R*R,
i=1,2,...,k,...l, j=1,2,...k,...l,
l - отношение размеров матрицы исходного изображения и подматрицы, равное N/R.
При таком представлении матричного умножения подматрица - клетка результата Xij вычисляется через сумму произведений подматриц
(8) 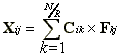
Оценим
общее время ДКП для случая
клеточного умножения матриц. В [8]
показано, что ускорение
параллельных вычислений при
умножении 2-х блоков размером
каждого R*R на R2
процессорах составит R2.
Полагая время умножения одной
клетки равным t1*R, а число
операций над клетками для двух
произведений (1) равным 2(N/R)3,
получим общее время ДКП для
вычислителя с p=R2 процессорами
равным
(9)
Эффективность
распараллеливания ДКП можно
повысить еще больше, если разбивать
изображение на блоки меньшего
размера и применять ДКП к отдельным
блокам, включающим M*M точек, где N
- кратное M. Это приводит к
некоторому увеличению сжатой
информации, которая уменьшается с
ростом M и минимальна при M=N
[3]. При M < N время выполнения
преобразования на
однопроцессорной ЭВМ составит .
Для времени преобразования
информации на p процессорах
получим
(10)
Следует отметить, что отношение (10) является более общим случаем (9) и при M=N они совпадают.
Распараллеливание этапа округления коэффициентов
ДКП предоставляет матрицу частотных коэффициентов для этапа округления. Стандарт JPEG реализует этот этап через матрицу округления Q, каждый элемент которой соответствует элементу матрицы ДКП. Обычно элементы матрицы Q увеличиваются в сторону увеличения индексов. На рисунке 2 представлен пример матрицы округления для блока 8*8 .
Рис.
2. Матрица округления Q
размером 8*8
Такой вид
матрицы позволяет на этапе
округления подавить высшие менее
значимые в изображении гармоники.
Результирующая матрица получается
делением каждого элемента матрицы
ДКП на соответствующий элемент
матрицы Q и последующем
округлением результата до
ближайшего целого числа. После
данного этапа преобразований
большое количество элементов
результирующей матрицы,
находящихся ближе к правому
нижнему углу превратятся в нули,
что увеличивает эффективность
упаковки. Степень параллелизма
алгоритма JPEG для этапа округления
равна количеству точек исходного
изображения(N*N). Время
выполнения этапа на
однопроцессорной ЭВМ составит , где t2 -
время выполнения операции деления.
Для p процессоров, с учетом
высокой степени параллелизма и
независимо от разбиения
изображения на блоки, это время
будет равно
(11) .
Распараллеливание
этапа кодирования
Это
заключительный этап работы
алгоритма JPEG, во время которого
коэффициенты округленной матрицы
обходятся зигзагом (Рис. 3).
Рис.
3. Обход зигзагом округленной
матрицы
При этом каждый последующий элемент кодируется как разница с предыдущим, чаще всего похожим на него. Нулевые значения кодируются с учетом повторов. Степень pаспараллеливания этапа равна единице, вследствие чего время выполнения кодирования как для однопроцессорной, так и для многопроцессорной ЭВМ составит
Т3(1)
= Т3(p) = t3*N2,
где t3 - время, необходимое на кодирование одного элемента матрицы. Распараллеливание данного этапа представляется возможным лишь для случая разбиения матрицы исходного изображения на блоки. При этом степень параллелизма будет равна числу блоков (N/M)2 . Тогда для оценки времени кодирования на многопроцессорной ЭВМ получим
(12) ,
если число процессоров p
меньше числа блоков , равного (N/M)2
и
(13) ,
если число процессоров p
больше числа блоков, равного (N/M)2
, то есть часть процессоров будет в
этом случае простаивать.
Суммарная
оценка эффективности
распараллеливания
Общее
время, необходимое для упаковки
изображения размера N*N, разбитого
на блоки размером M*M каждый,
составит на многопроцессорной ЭВМ
T(p,M)=
T1(p,M) + T2(p,N) + T3(p,M),
где T1(p,M),T2(p,N),T3(p,M) - времена соответственно этапов ДКП, округления и кодирования, вычисляемые по формулам (10) - (13).
В системе Mathcad построены
графики зависимости времени
упаковки изображения T(p,M),
ускорения s(p) и эффективности e(p)
от числа процессоров p
вычислителя для обработки матрицы
экрана 256*256 пикселов при
допущении, что коэффициенты t1 = t2 =
t3 = 1. Эти зависимости
представлены на рисунках 4,5,6,7 для
двух случаев: при применении
кодирования ко всему изображению (M=N)
и при разбиении исходного
изображения на блоки ( M<N).
Рис. 4.
Временные оценки этапов упаковки
при отсутствии разбиения на блоки
(M=N)
Рис.
5. Ускорение и эффективность
распараллеливания при отсутствии
разбиения изображения на блоки (M=N=256)
Представленные
на графиках результаты
распараллеливания демонстрируют
достаточно высокие значения
ускорения и эффективности в
широком диапазоне изменения числа
процессоров. При этом значение
ускорения не сильно меняется при N<p<N2
. Разбиение исходной матрицы на
блоки позволяет получить
значительно большие значения
ускорения и эффективности, так как
в этом случае эффективно
распараллеливаются все три этапа
упаковки.
Рис.
6. Временные оценки этапов упаковки
при разбиении изображения на блоки
(M<N).
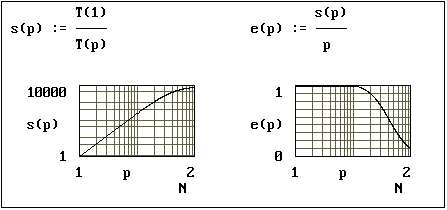
Рис.
7. Ускорение и эффективность
распараллеливания при разбиении
изображения на блоки (M=16, N=256)
Заключение
Таким образом
можно утверждать, что
последовательные схемы вычисления
алгоритма упаковки графической
информации позволяют адаптировать
его к параллельному без разработки
специальных новых алгоритмов. Это
связано с возможностью
представления рассмотренных схем
вычислений в виде стандартных
матричных операций, реализованных
на современных архитектурах
многопроцессорных вычислителей. В
работе показано, что при
параллельном исполнении алгоритма
упаковки достигается многократное
ускорение вычислений в широком
диапазоне изменения числа
процессоров. Полученные результаты
позволят сделать правильный выбор
архитектуры вычислителя и
программных средств для решения
данной задачи. Подробный анализ
аппаратно - программных средств для
реализации алгоритма упаковки
графической информации будет
представлен в отдельной статье.
Литература
1.
Поммерт А., Пфлессер Б. Визуализация
объема в медицине //Открытые
системы. - 1996. - № 5. - С.56-61.
2. Головкин Б. А. Вычислительные
системы с большим числом
процессоров. -М.: Радио и связь,1995. 3.
Wallace G.K. The JPEG Still Picture. Compression Standard //
Communication of the ACM. 1991. V.34. № 4.4. Мастрюков
М. Алгоритмы сжатия информации.
Часть 7. Сжатие графической
информации. //Монитор. -1994.- № 6.- С.12-20.
5. Хокни Р., Джессхоуп К.
Параллельные ЭВМ. - М.: Радио и связь,
1986.
6. Мунерман В. И., Самойлова Т.А.
Параллельные вычисления в задаче
размещения БИС. //Сборник научных
трудов МЭИ.- Смоленск, 1995. - С.85-89.
7. Гендель Е. Г., Мунерман В.И.
Применение алгебраических моделей
для синтеза процессов обработки
файлов. // Управляющие системы и
машины. - № 4. - 1984.
8.Прангишвили И.В.,
Виленкин С. Я., Медведев И. Л.
Параллельные вычислительные
системы с общим управлением. - М.:
Энергоатомиздат, 1983.
Кафедра
вычислительной техники
Смоленский государственный
педагогический института им.
К.Маркса
Поступила в редакцию 27. 02. 97.