
МОРФОЛОГИЯ
И КИБЕРНЕТИКА
УДК 51
©
1997 г. В. М. Балк
История развития современной цивилизации является одновременно историей математики - науки, основанной на абстракциях. Формальная логика, применяемая к абстрактным объектам и лежит в основе большинства достижений научно-технического прогресса. Однако большей части человечества свойственно не абстрактное, а образное мышление. Следствием этого является постоянное стремление математиков придать своим рассуждениям наглядный, обычно геометрический или физический смысл.
Например, интеграл трактуется как площадь фигуры, производную - связывают с касательной к кривой и т.д. Примеры такого создания содержательных иллюстраций приведены, например, в работе [1]. Однако существуют области математики, где наглядность заложена в саму основу, в свойства исследуемых объектов.
Одна из них
- теория графов- возникло в конце XVIII
века из известной работы Эйлера
(“задача Леонарда Эйлера о
кенигсбергских мостах” 1736 г,
подробнее см. [2]) и в настоящее время
превратилось в весьма мощный и
непрерывно развивающийся
математический инструмент. Автор
предполагает в данном очерке дать
читателям концептуальное
представление о графах.
Основные
понятия
Первое из
основных понятий теории графов -
это понятие вершины. В теории
графов оно принимается в качестве
первичного и не определяется. Его
нетрудно представить себе на
собственном интуитивном уровне.
Обычно вершины графа наглядно
изображаются в виде окружностей,
прямоугольников другими фигурами
(рис.1).

Рис.
1
Хотя бы одна вершина должна обязательно присутствовать в каждом графе.
Другое
основное понятие теории графов -
дуги. Обычно дуги представляют
собой отрезки прямых или кривых,
соединяющих вершины. Каждый из двух
концов дуги должен совпадать с
какой-нибудь вершиной. Случай,
когда оба конца дуги совпадают с
одной и той же вершиной, не
исключается. Например, на рис.2 -
допустимые изображения дуг, а на
рис.3 - недопустимые:
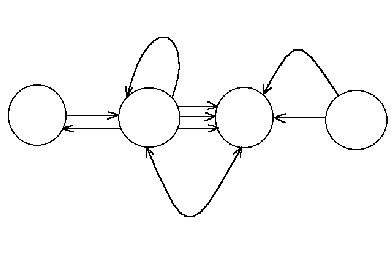
Рис. 2
Рис. 3
В теории графов используются дуги двух типов - ненаправленными или направленными (ориентированными). Граф, содержащий только ориентированные дуги, называется ориентированным графом или орграфом.
Дуги могут быть однонаправленными, при этом каждая дуга имеет только одно направление, или двунаправленными.
В
большинстве применений можно без
потери смысла заменить
ненаправленную дугу на
двунаправленную, а двунаправленную
- на две однонаправленных дуги.
Например так, как показано на рис. 4.
Рис. 4
Как
правило, граф либо сразу строится
таким образом, чтобы все дуги имели
одинаковую характеристику
направленности (например, все -
однонаправленные), либо приводится
к такому виду путем преобразований.
Если дуга AB- направленная, то это
значит, что из двух ее концов один (A)
считается началом, а второй (B) -
концом. В этом случае говорят, что
начало дуги AB есть вершина A, а конец
- вершина B, если дуга направлена от A
к B, или что - дуга AB исходит из
вершины A и входит B (рис. 5).
Рис. 5
Две вершины графа, соединенные какой-либо дугой (иногда, независимо от ориентации дуги) называют смежными вершинами.
Важным понятием при исследовании графов является понятие пути. Путь A1,A2,...An определяется как конечная последовательность (кортеж) вершин A1,A2,...An и дуг A1, 2,A2 ,3,...,An-1, n последовательно соединяющих эти вершины.
Важным понятием в теории графов является понятие связности. Если для любых двух вершин графа существует хотя бы один соединяющий их путь - граф называется связным.
Например, если изобразить в виде графа систему кровообращения человека, где вершины соответствуют внутренним органам, а дуги - кровеносным капиллярам, то такой граф, очевидно, является связным. Можно ли утверждать, что система кровообращения двух произвольных людей является несвязным графом? Очевидно, нет, поскольку в природе наблюдаются т. н. “сиамские близнецы”.
Связность может быть не только качественной характеристикой графа (связный/несвязный), но и количественной.
Граф называется K-связным, если каждая его вершина связана с K других вершин. Иногда говорят о слабо- и сильносвязанных графах. Эти понятия субъективны. Исследователь называет граф сильносвязанным если для каждой его вершины количество смежных вершин, по мнению исследователя, велико.
Иногда связность определяют как характеристику не каждой, а одной (произвольной) вершины. Тогда появляются определения типа: граф называется K-связным, если хотя бы одна его вершина связана с K других вершин.
Некоторые авторы определяют связность как экстремальное значение количественной характеристики. Например, граф является K-связным, если в графе существует хотя бы одна вершина, связанная с K смежными вершинами и не существует ни одной вершины, связанной с более чем K смежными вершинами.
Например,
детский рисунок человека (рис. 6)
представляет собой граф с
максимальной связностью равной 4.
Рис. 6
Еще одна характеристика графа, исследуемая в ряде задач, часто называется мощностью графа. Эта характеристика определяется как количество дуг, связывающих две вершины. При этом дуги, имеющие встречное направление, часто рассматриваются раздельно.
Например, если вершины графа представляю собой узлы обработки информации, а дуги - однонаправленные каналы передачи информации между ними, то надежность системы определяется не суммарным количеством каналов, а наименьшим количеством каналов в любом направлении.
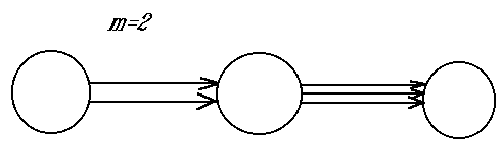
Рис.
7
Мощность, как и связность, может определяться как для каждой пары вершин графа, так и для некоторой (произвольной) пары.
Существенная характеристика графа - его размерность. Под этим понятием обычно понимают количество вершин и дуг, существующих в графе. Иногда эта величина определяется как сумма количеств элементов обоих видов, иногда - как произведение, иногда - как количество элементов только одного (того или иного) вида.
Размерность графа особенно следует учитывать при компьютерной обработке модели.
Решение некоторой предметной задачи можно достигнуть двумя путями. Можно исследовать сам предмет, делая умозаключения о сущности предмета на основе прямых измерений или наблюдений. Например, сравнивая кровь из вены и артерии можно увидеть различия в цвете и, на основании такого прямого наблюдения, утверждать, что химический состав проб - различен.
Такой путь в большинстве наук дает, в основном, только простейшие, тривиальные результаты.
Другой путь состоит в построении математической модели изучаемого предмета и исследовании этой абстракции с целью получения умозаключений о сущности предмета, основанных на свойствах модели.
При этом сразу же возникает вопрос: достоверна ли модель? Отражает ли она существенные, с точки зрения исследователя и получаемых результатов, свойства моделируемого объекта?
Общего решения здесь нет. Обычно споры о достоверности модели продолжаются до тех пор, пока с ее помощью не удастся не только объяснить наблюдаемые явления, но и предсказать новые, еще неизвестные, факты. Экспериментальное подтверждение этих фактов обычно является и подтверждением достоверности модели.
Математическая модель строиться в рамках того или иного раздела математики, наследуя при этом свойственные данному разделу ограничения.
Принципиально существенным свойством графов как инструмента моделирования является их дискретность.
Вершина либо есть, либо ее нет. Дуга, связывающая две конкретные вершины, либо существует, либо нет. Не бывает половины дуги или четверти вершины. Такой дискретный подход к моделированию имеет как достоинства, так и недостатки.
К достоинствам следует отнести “навязывание” исследователю необходимости выделения существенного в исследуемом объекте и “отсечения” бесконечного количества мелочей.
К недостаткам - принципиальная невозможность моделирования таким способом непрерывных процессов.
Если все-таки модель должна быть непрерывной следует сменить используемую математику. Дифференциальное или интегральное исчисление, основанные на понятии бесконечно малых величин, достаточно хорошо разработаны и оперируют непрерывными функциями.
Человеческому мышлению, видимо, одинаково свойственны как понятие непрерывности, так и понятие дискретности. Пример тому - использование термина “квант” (т.е. дискретный элемент) в различных областях знаний (квант света, квант крови [3] и т.д.).
Рассмотрим пример (рис. 8, 9). Результаты измерение давления пациента могут быть представлены в виде графика непрерывной функции. А можно абстрагироваться от цифровых данных и выделить существенные моменты. Пусть вершина A соответствует нормальному давлению, B - повышенному, С - инсульту.
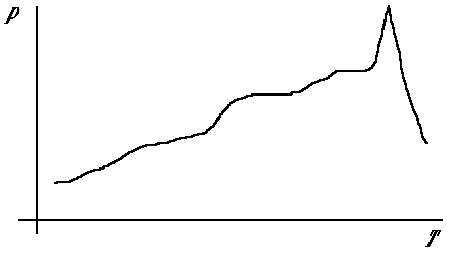
Рис. 8
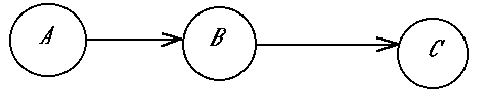
Рис.
9
Если этот граф соответствует действительности, то можно утверждать, что инсульт не может наступить при нормальном давлении. А если справедлива другая модель (рис.10) - может.
Рис. 10
Дискретность есть общее свойство всех графовых моделей, но часто этого ограничения недостаточно. Чем больше ограничений (в разумных пределах!), основанных на сути моделируемой задачи, наложено на модель, тем больше шансов получить содержательный результат.
Например, если вершины графа представляют собой узлы (бифуркации и соустья) кровеносной системы, то можно сформулировать следующее ограничение : связность графа, моделирующего кровеносную систему не более 3 [3].
Первый шаг при построении модели - определение соответствия между элементами изучаемого объекта и элементами модели (вершинами и дугами графа). Здесь можно выделить два основных подхода.
Первый можно условно назвать “географическим”. При этом граф строиться похожим на “географию” моделируемого объекта.
Другой
подход можно назвать
“состоятельным”. При этом граф
представляет собой изображение
процесса изменения состояний
объекта. Например, на рис. 6 - граф,
изображающий человечка. На рис. 11 -
изменения этого графа при
последовательной ампутации
конечностей, например, при
облитерирующем эндартериите или
атеросклерозе. Этот процесс
последовательной “ампутации”
может быть изображен графом на
рис.12.
Рис. 11
Рис. 12
Обычно, начиная исследования, строят “географическую” модель, поскольку она часто представляется более наглядной. При достижении достаточного уровня знаний процессов, происходящих в исследуемом объекте, часто переходят к “состоятельным” графам. И, наконец, иногда оказывается полезным построить обе модели и, связав их между собой, исследовать оба графа одновременно.
Построив модель, т. е. определив правила соответствия между элементами, объекта и элементами модели, исследователь надеется сразу воспользоваться результатами труда математиков, доказавших в отношении таких моделей те или иные утверждения. Например, строим модель кровообращения, получаем некоторый граф. Из математических трудов узнаем, что графы такого рода являются ациклическими (т.е. не содержат путей, у которых начало и конец совпадают с одной и той же вершиной). Вывод - из человека непрерывно вытекает кровь.
Для того, чтобы воспользоваться результатами доказанных математиками утверждений, необходимо чтобы построенная модель соответствовала тому типу графов, для которого это утверждение доказано. Для того, чтобы воспользоваться результатами математических исследований, приходится, иногда, вносить в модель некоторые изменения, не изменяющие достоверности соответствия модели объекту, но приближающие ее к типам графов, исследованных математически.
Объекты, моделируемые графами, имеют весьма разнообразную природу. Стремление отразить эту специфику привело к описанию большого количества разновидностей графов. Процесс этот продолжается и в настоящее время. Многие исследователи для своих конкретных целей вводят новые разновидности и выполняют их математическое исследование с большим или меньшим успехом.
В основе
всего этого многообразия лежат
несколько довольно простых идей, о
которых мы здесь и будем говорить.
Окраска
Окраска графов - весьма популярный способ модификации графов.
Этот прием позволяет и повысить наглядность модели и увеличить математическую нагруженность. Способы введения окраски могут быть различными. По тем или иным правилам окрашиваются как дуги, так и вершины. Окраска может быть однократно определена или меняться с течением времени (т.е. при приобретении графом каких-либо свойств); цвета можно преобразовывать по тем или иным правилам, и т.д.
Например,
пусть граф представляет собой
модель кровообращения человека,
где вершины соответствуют
внутренним органам, а дуги -
кровеносным капиллярам. Окрасим
артерии в красный цвет, а вены - в
синий. Тогда очевидно
справедливость следующего
утверждения - в рассматриваемом
графе (рис.13) существуют, и при этом
только две, вершины, имеющие
исходящие красные дуги (на рисунке
красный цвет изображен жирно).
Рис.
13
Взвешенность
Часто дугам или вершинам приписывают количественную характеристику - “вес”. Это позволяет выполнять в модели не только качественный, но и количественный анализ. Например, если вершина графа соответствует узлу электрической сети, а дуги - протекающим в сети токам, то взвесив дуги величиной соответствующего тока можно сформулировать следующее утверждение:
для каждой
вершины графа сумма весов дуг,
входящих в вершину равна сумме
весов дуг исходящих из вершины. Это
утверждение известно из курса
школьной физики как правило
Кирхгофа.
Дольность
Иногда элементы объекта, моделируемые вершинами, имеют существенно различный характер. Или к реально существующим в объекте элементам в процессе формализации оказывается полезным добавить некоторые фиктивные элементы.
В этом, и некоторых других случаях, вершины графа естественно разделить на классы (доли). Граф, содержащий вершины двух типов, называют двудольным и т.д. При этом в число ограничений графа вносятся правила, касающиеся взаимоотношений вершин разных типов. Например: “не существует дуги, которая бы соединяла вершины одного типа”. Одна из разновидностей графов такого рода называется “сеть Петри” (рис. 14) и имеет достаточно широкое распространение. Более подробно сети Петри будут рассмотрены в следующей статье этого цикла.
Понятие
дольности может быть применено не
только к вершинам, но и к дугам.
Рис. 14
Хотя эти идеи позволяют строить весьма разнообразные графы, не следует терять чувство меры.
Во-первых, математика стремиться к обобщениям и, построив чересчур “изощренную” модель, исследователь рискует не найти в литературе готовых результатов.
Во-вторых, при построении такой модели достаточно легко попросту запутаться.
В третьих,
“изощренность” модели усложняет
ее компьютерную обработку.
Графы, как и многие другие математические модели, можно исследовать двумя разными методами.
Традиционный математический подход состоит в формулировании некоторого утверждения о свойствах рассматриваемого графа и доказательства его истинности методами логики. Примеры утверждений такого рода (естественно, чисто иллюстративного уровня) разбросаны по тексту выше.
Другой подход основан на компьютерной обработке модели.
При этом, сформулированное утверждение доказывается в результате действий программы, преобразующей и анализирующей цифровое описание графа.
Так же, как и в традиционной математике, компьютерная обработка может доказать справедливость утверждения или его ложность, или не дать определенного заключения.
Существенное отличие компьютерного доказательства от традиционного математического состоит в том, что в каждый момент времени в памяти компьютера находится один конкретный экземпляр графа, а не все множество всевозможных экземпляров, допускаемых правилами построения модели, рассматриваемых при доказательстве математиком.
Поэтому, для получения доказательства, следует предпринять меры для генерации компьютером всех возможных вариантов модели. Затем, исследуя каждый вариант из этого множества можно получить подтверждение истинности утверждения.
Вопрос об уменьшении количества рассматриваемых экземпляров и методах их порождения в данной статье не рассматривается и относиться к вопросам оптимизации. (См. например, [4]). Здесь же следует сказать несколько слов о способах компьютерного описания графа.
Обычно граф описывается т.н. матрицей смежности. При этом все вершины нумеруют. Если i-ая вершина связана дугой с j-ой вершиной, то такие вершины называют смежными, а в матрице смежности в ячейке, соответствующей i-ому столбцу и j-ой строке ставится отметка.
Матрица смежности допускает различные модификации - в зависимости от типа описываемого графа, решаемых на матрице задач анализа и используемых алгоритмов.
Если мощность графа равна 1 или существенен только факт связи вершин, но не количество дуг, их связывающих, - отметка в соответствующей ячейке матрицы может иметь логический тип (ДА/НЕТ, TRUE/FALSE).
Если необходимо учесть количество дуг, связывающих конкретную пару вершин, но граф не ориентирован, - отметка получит значение из ряда натуральных чисел.
При описании орграфа, т.е. в ситуации, когда следует различать дуги, входящие в вершину, и дуги, исходящие из вершины, - отметка может иметь значения из ряда целых чисел (включая отрицательные).
При использовании взвешенных дуг каждой ячейке матрицы должен соответствовать ряд чисел, состоящий из значений присвоенных весов. Такое описание графа может быть представлено в виде трехмерной матрицы.
Введение окраски дуг можно учесть перейдя к четырехмерной матрице, где дополнительный слой содержит номер цвета для каждой дуги.
Получив матрицу связности можно приступить к ее анализу. Методы матричного исчисления достаточно хорошо проработаны [7]. Однако, многие содержательные выводы могут быть получены более просто, если использовать математические методы не “в лоб”, а помня о свойствах графа, описываемого матрицей.
Например, если граф не ориентирован, и A - его матрица смежности, то, очевидно:
a i,j є a j,i
Т.е. половина ячеек матрицы содержат дублирующую информацию (матрица симметрична относительно главной диагонали).
Иногда вместо матрицы, где индексы соответствуют номерам вершин, используют матрицу, описывающую дуги. Т.е. дуги нумеруются и каждая строка такой матрицы состоит из двух ячеек, содержащих номера вершин, связанных данной дугой. Ячеек только две, поскольку у дуги может быть только одно начало и один конец. В отличии от вершины, которая может быть связана с множеством “соседок”. Этот подход оказывается, иногда более удобным. Обычная матрица смежности - квадратная. Матрица дуг может быть представлена в виде двух линейных массивов, что упрощает, в частности, компьютерную обработку.
Графы, как инструмент моделирования, обладают существенными достоинствами:
1) - наглядность;
2) - гибкость;
3) - дискретность.
Основные стадии процесса использования графовых моделей можно представить так:
1) - анализ объекта и построение графа;
2) - анализ графа и построение описывающей матрицы;
3) - компьютерный анализ матрицы и формирование суждений об истинности выдвинутых гипотез.
Итерационность использования графовых моделей допускается как на уровне процесса в целом, так и на уровне отдельных стадий.
Сам
процесс использования графов
представлен в виде графа на рис. 15.
Рис.
15
ЛИТЕРАТУРА
Балк М. Б., Болтянский В. Г. Геометрия масс. - М.,1987.
Перельман Я. И. Занимательная геометрия.-М.-Л.:ГИТТЛ,1957. - С. 242-243.
Глотов В. А. Структурный анализ микрососудистых бифуркаций. - Смоленск:Амипресс, 1995. - 255 с.
Майника
Э. Алгоритмы оптимизации на
сетях и графах. /Под ред.
Е.К.Масловского - М.: Мир,1981. - 322 c.
Смоленский гуманитарный университет
Поступила в редакцию 11.04.97.