
УДК
611:6П215]+615.017
УПРАВЛЯЮЩИЕ МЕДИКО-БИОЛОГИЧЕСКИЕ
СИСТЕМЫ
В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
(ВОЗМОЖНОСТЬ ПРИМЕНЕНИЯ ТЕОРИИ УПРАВЛЕНИЯ
СИСТЕМАМИ В МЕДИКО-БИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ)
©1997 г. И.
А.Платонов
При
рассмотрении медико-биологической
системы (МБС) возникает проблема
многокритериальности: задача
выбора решения при наличии
нескольких функций цели. Введя
определенные ограничения при
аппроксимации МБС, удается найти
оптимальные критерии, обобщающие
определенный набор векторов
возмущающих факторов. Это
позволяет в целостной МБС выделять
совокупность взаимодействующих
подсистем. Минимальным числом
таких подсистем в целостной МБС
может быть три: возмущающие факторы
физиологические - f0(t)
x(t), патогенетические - f1(t)
x(t) и лечебные - f2(t) x(t).
Это позволяет наметить пути к
решению задачи управления МБС в
условиях неопределенности.
Организм - как биологическая система (БС) постоянно воспринимает какие-то внешние воздействия. Любая система, в том числе и биокибернетическая, характеризуется определенным набором входных [x(t)] и выходных [y(t)] параметров (сигналов). Величины этих параметров в БС представляют собой какие-то входные и выходные биологически значимые определенные функции.
При
изучении поведения сложных
объектов, каким является БС,
подходящей и адекватной моделью
может являться хорошо себя
зарекомендовавшая в
кибернетических исследованиях
модель "черного ящика".
Построение такой модели основано
на принципе: оптимальное
управление системой возможно при
неполной информации. Это можно
представить в виде общепринятой
схемы:

или в
математическом виде:
y =
f(x1, x2, ... ,x k),
где x1 -xk - факторы-входы; y - параметр оптимизации или функция отклика.
Всегда можно представить, что на БС действует какой-то внешний фактор f(t), зависящий от времени t и фиксированный (определен нами в момент t). Тогда можно считать, что f(t) непрерывна по t, а f(t)Ix(t). Такими возмущающими факторами являются различные биологически значимые сигналы, в том числе как патогенные, так и лечебные. В этом случае следует говорить не просто о БС, а о медико-биологической системе (МБС).
Для перехода от "реальной" МБС к абстрактной математической модели, использующей принцип "черного ящика", приемлемым может являться метод аппроксимации (аппроксимирования).
Сформулируем в общем виде задачу аппроксимации "черного ящика".
Пусть входные величины (параметры, возмущающие факторы) обозначим x (x1, x2, ... , xn), а выходные - (y1, y2, ... , yk). При этом условие n = k может и не соблюдаться. Пусть также в некоторые фиксированные моменты времени t0, t1, ..., tj данные параметры принимают значения xi и yi (i = 0, 1, ..., j).
Тогда можно сформулировать такое правило, в соответствии с которым входные функции x(t) БС определяют ее выходные функции y(t). Такое правило будет представлять оператор системы - ОС. Математическую зависимость между входом и выходом такой БС (МБС) можно записать с помощью ОС - L:(1) y(t) = L{x(t)}.
Сформулированное правило (L) представляет собой ничто иное как математическую ОС (МОС) - множество абстрактных элементов, отображающих биологические факторы, и действие над ними.
У такой МОС есть четкие внутренние побуждающие мотивы и цели: расширение и выполнение операций и охват всего того, что желаем описать.
При формулировании правила L на МОС налагаются определенные ограничения, связанные с действием БС не по абстрактным законам, принятым в математическом языке МОС, а по определенным законам биологии. Кроме того, медицинские аспекты проблемы функционирования БС также налагают свои законы. Таким образом, правило L и МОС как бы неоднозначны. Для разрешения сложившейся ситуации по-видимому более корректно следует говорить не о МОС как таковой, а о "медико-биологической" МОС (МБ МОС). В такой ситуации множества уже не будут составлять абстрактные элементы, ибо они приобретают конкретные биологические функции, а операции подчинены определенным биологическим законам (биологически значимому смыслу).
Все сказанное не является противоречием для языка МОС, а только уточняет область применения МОС в медико-биологических исследованиях. МБ МОС представляет совокупность математических операций, отражающих и эквивалентных "работе" БС. Такая ОС позволяет по данным значениям возмущающих факторов x(t) найти функции-отклики y(t).
БС по своим характеристикам являются динамическими: значение y(t1) зависит как от значения X в момент t1, так и от интервала Dt, прошедшего с момента t0 (начала воздействия) до t1 ( Dt = t1 - t0). Нахождение решающего правила - оператора L, в случаях описания МБС чрезвычайно затруднено.
При рассмотрении поведения МБС наибольший интерес представляет вычленение двух групп факторов возмущения - патогенных f1(t) и лечебных f2(t).
При действии возмущающих факторов f1(t) начало воздействия в момент t0, как правило, установить довольно трудно. В связи с этим значение Dt остается неопределенным (не установленным). Решением этого вопроса может быть подбор столь малого временного интервала , что его значением можно пренебречь: lim Dt®t при t®0. Практически в этом случае возможно рассматривать в статике динамическую МБС. Тогда для любого момента t справедливо однозначное соответствие X~Y или f(t)~y(t) при f(t)Ix(t).
При построении математической модели (ММ) МБС требуется количественная формулировка цели исследования, которая фактически представляет собой параметр оптимизации (функция цели, критерий оптимизации).
Набор параметров оптимизации можно рассматривать как вектор, компонентами которого являются отдельные параметры. Тогда формула (1) можно записать в виде соотношения векторов:
(2) Y = L ? X.
Взаимосвязь между входом и выходом может осуществляться двумя основными путями. Так, возможно однозначное соотношение между входными (X) и выходными (Y) векторами:
Такой вариант работы МБС в реальных условиях чрезвычайно редкий.
Другой путь взаимосвязи: неоднозначные соотношения между векторами входа и выхода.
Набор m векторов X, принадлежащих векторному множеству A может давать единичное значение выхода Yk:
(4) m{X} I A ® Yk0.
В то же время выходной вектор Xi вызывает активацию (набор) целого подмножества функций из множества B:
(5) Xi ® M{Y}I B.
Каждый из этих вариантов (4) и (5) равновероятен для функционирования МБС. Так, например, ряд инфекционных агентов (патогенные микроорганизмы), физический фактор - гипертермия, лечебный фактор - препарат очищенной серы (сульфозин), способны вызвать повышение температуры тела. В то же время лекарственный препарат (ЛП) - атропина сульфат (из группы М-холиноблокаторов), оказывает влияние на ЦНС, ЖКТ, мочевыводящие пути и другие системы организма.
Системы, когда нет однозначного соотношения между параметрами входа и выхода, как правило, являются нелинейными и требуют довольно сложного аппарата МОС. Решение таких систем возможно при изучении абстрактных систем, имеющих строгие границы. В то же время МБС - система вероятностная.
Решение МБС в этом случае будет носить скорее нелинейный характер, т.е. в каждом отдельном случае требует громоздкого подбора частных стационарных решений.
При возникновении ситуации с несколькими параметрами оптимизации надо стремиться к уменьшению его числа.
Таким образом, при рассмотрении МБС возникает проблема многокритериальности -задача выбора решения при наличии нескольких функций цели. Под функцией цели в данном случае понимаем такую функцию (критерий оптимизации), наименьшее или наибольшее значения (возмущающие факторы МБС) которых ищутся в задаче с учетом имеющихся для данной БС ограничений. Подбор таких критериев оптимизации будет определять эффективность аппроксимированной нами МБС.
Такой путь при аппроксимации МБС реален. В приведенных примерах все возмущающие факторы или выходные функции системы могут быть объединены.
Так, при m{X} - множестве входных факторов, в первом примере они могут быть объединены, ибо несмотря на их качественные различия, эти возмущающие факторы имеют общую точку действия - центр терморегуляции (Y). Во втором случае, когда имеется один входной возмущающий фактор Xi - ЛП, вызывающий разнообразные выходные эффекты [M{Y}IB], имеется также общая структурно-функциональная подсистема - холинергический рецептор.
Следовательно, введя определенные ограничения при аппроксимации МБС, удается найти оптимальные критерии, обобщающие определенный набор векторов возмущающих факторов. При этом главное требование, которому должен удовлетворять выбранный параметр оптимизации, - адекватное измерение (отражение) эффективности аппроксимированного объекта.
В такой ситуации естественно идти к задаче моделирования ограничений от тех практических целей, для которых создается ММ. В этом случае имеет смысл приходить к линейным системам, ибо для них справедлив принцип суперпозиции. Тогда реакция системы на любую линейную комбинацию входных возмущающих факторов равна такой же линейной комбинации реакций системы на каждое отдельное воздействие. Следовательно любой набор из m векторов и сi их весах и любой входной (возмущающих факторов) функции xi(t) можно представить:
(6)
Это позволяет в целостной МБС выделять совокупность взаимодействующих подсистем. Минимальным числом таких подсистем в целостной МБС может быть три: возмущающие факторы физиологические - f0(t) М x(t), патогенетические - f1(t) М x(t) и лечебные - f2(t) М x(t).
Будем рассматривать всю совокупность f0(t) как возмущающие факторы, поддерживающие нормальные, физиологические функции ИБС. В эту группу будем включать и адаптивные возмущающие факторы. В противоположность сказанному имеются факторы f1(t), вносящие отрицательное воздействие на БС, приводящие к развитию патологического процесса - болезни. Действие возмущающих факторов имеет направление от входа к выходу и связь между ними носит прямой характер (прямые связи).
Любая система, в том числе и МБС, должна "знать" о состоянии уровня своего функционирования и вносить какие-то изменения. Поэтому важным компонентом такой системы является обратная связь, позволяющая эффективно реализовать управление выходными функциями. Все БС на любом уровне своего функционирования имеют обширную структуру регулирования входных параметров. Такие структурно-функциональные образования имеют запас надежности, казалось бы, превышающий необходимый. Так, в мозге максимально может функционировать до 1011 имеющихся на данный момент нейронов, но "работает" в каждый временной промежуток значительно меньше [3].
Это и позволяет при воздействии f1(t) МБС сохранять свою жизнеспособность. Тем не менее, в определенной ситуации внутренних управляющих факторов оказывается недостаточно и развивается предболезнь. Введение в этот момент ЛП [возмущающий фактор f2(t)] может предотвратить дальнейший дефицит в управлении - развитие патологического процесса. Возможен и другой вариант: ЛП ослабляет управляющее влияние внутренних факторов (неверный подбор препаратов, недоучет патогенного фактора, неверная комбинация препаратов и т.д.).
Препарат - биологически активный агент, в силу своих особенностей способен также выступать как синергист патологического фактора или антагонист физиологического фактора. Это обусловлено индивидуальной структурой вещества, имеющего биологически активные реактивные группы. Такая ситуация особенно характерна для структурно-сложных биологически активных веществ, например, регуляторных пептидов. Тогда ЛП f2(t) уже может стать синергистом патогенного фактора f1(t) [2].
Попробуем описать биокибернетическую систему - аналог БС, в виде определенной схемы, используя элементы теории автоматического управления - ТАТ.
В
идеальном случае (абстрактная,
замкнутая на себя БС) имеется
какая-то группа факторов (Q),
запускающих (генерирующих) такую
систему. Такой фактор действует
через звено управляющей подсистемы
(УПС) на объект управления -
биологический объект управления (БОУ).
Регулирование в данной БС
осуществляется через звено
обратной связи - подсистему,
обеспечивающей управляющую
обратную связь (ПУОС).
Представим такую БС в виде
графических элементов (схема 2).
Схема будет иметь классическую
структуру, описываемую в теории
управления систем.
Такая идеальна система, является закрытой (работает на себя) и не имеет биологического смысла.
В БС, не имеющей каких-либо других возмущающих воздействий, Q - внутренний фактор, обеспечивающий функционирование системы в целом (задающий фактор внутренней среды), имеет постоянство. В этом случае (рассогласование) будет равно нулю. Такая схема (система) схоластична и в ней, в принципе, отпадает потребность во всех элементах управления.
В реальных условиях на БС, в том числе и на МБС, действуют различные биологически (физиологически) значимые факторы f0(t), определяющие биологический смысл ее существования - переработку информации и активное влияние на среду. Такие системы по своей сути являются открытыми.
В таком
случае возникает потребность в
определенной коррекции
"работы" БОУ и в подсистеме
управления им. В ином случае БС не
способна была бы выполнять свои
функции. В результате
жизнедеятельности [влияние Q и f0(t)]
БС "отвечает" какой-то
функцией y(t) и формируется
эквивалентная регулируемая
величина yоб [y(t) ~ yоб],
которая и определяет сигнал
обратной связи - yос. Далее
через элемент сравнения формирует
величина e (e
= Q yос), управляющая входом УПС
и формированием управляющего
воздействия [u(t)] на БОУ. В
физиологических условиях
(нормальных условиях-параметрах)
величина u является достаточным и
адекватным управляющим
воздействием для поддержания
обычных параметров
жизнеспособности БС. В реальных
условиях жизнедеятельности
существует какая-то величина s , ограничивающая
биологические возможности системы.
При этом, исходя из биологического
смысла функционирования МБС,
должно соблюдаться условие u?s . Выходная функция
y(t) при таких условиях находится в
пределах обычных, нормальных
колебаний (область нормальных для
БС векторов). Кроме физиологических
возмущающих факторов f0(t) на
МБС действуют патогенные факторы - f1(t).
Такие возмущающие факторы
суммируются и представляют уже
новую функцию - , оказывающую
действие на БОУ:
(7) a{f0(t), f1(t)}.
Функция a в данном случае
является интегральной и чаще не
представляет простую сумму f0(t)
и f1(t), ибо конечные
биологические проявления данной
функции при взаимодействии
довольно сложны: от синергизма до
антагонизма:
f0(t) + f1(t)
(8) a= f0(t) - f1(t)
a1f0(t) + a2
f1(t),
где a1 и a2 коэффициент потенцирования.
При воздействии f1(t) возможны две ситуации. Так, интегрированное воздействие всех возмущающих факторов не вызывает превышение предела величины e, что позволяет управляющей системе "удерживать" БОУ в пределах биологических (нормальных) параметров - Y0 (Y0 М FFI БС, где FF - область нормальных биологических функций).
При истощении биологических резервов воздействие f1(t) может привести к превышению адаптационных возможностей МБС. В этом случае s < u, что приводит к появлению нового состояния y1(t), патологическому ( Y1М PF IМБС, где PF - область патологических функций).
В этом случае требуется внешнее воздействие для стабилизации системы (т.е. приведению к условию s?u ). Для МБС это будут лечебные воздействия. Одним из вариантов такого воздействия является применение ЛП [f2(t)].
В такой ситуации возможны следующие варианты.
1. ЛП ведет к компенсации патологического процесса (s?u ®Y0I FF).
2. ЛП ведет к дальнейшей декомпенсации, т.е. s<u ®Y1PF [синергизм между f1](t) и f2(t)].
3. ЛП недостаточно эффективны и не удается достигать компенсации [антагонизм между f1(t) и f2(t), но возмущающее действие f2(t) недостаточно], т.е. остается верным условие: s<u.
4. ЛП не оказывает влияние на управляющую систему (ЛП подобран неверно) и s<u.
В данном случае для биокибернетической МБС указанные варианты распались на две группы: эффективные и неэффективные для управления. В биологическом отношении это будет соответствовать: поддержанию и невозможности поддержания жизнеобеспечения (жизнеспособности ) МБС.
Представим
изложенное в виде графических
элементов (схема 3):
Представленная схема работы МБС уже имеет, по сравнению со схемой 2, реальную биологическую аналогию и позволяет рассматривать конкретные процессы.
В результате работы указанной схемы (схема 3) появляется корригированная управляющая величина g:
(9) g = u + af2(t),
где коэффициент "a" зависит от синергизма (a=1) или антагонизма (a = 1) в действии a и f2(t). В случае, если возмущающий фактор f2(t) индифферентен как управляющий, то a=0.
В описанной биокибернетической системе внутренний (генерирующий) возбуждающий фактор является постоянным и неизмененным (Q=const), а внешние возмущающие факторы, как это уже было рассмотрено, изменяются от времени: x(t).
При этом x(t)=f(g,a). Входящие функции-параметры зависят от ряда возмущающих факторов [f0(t), f1(t), f2(t)], которые условно (искусственно) вычленены из всего множества существующих биологических факторов. Введем при каждом возмущающем факторе коэффициент b", имеющий разные биологические значения в зависимости от конкретных (реальных) условий функционирования (работы) МБС.
Пусть: b=0, если фактор отсутствует; b=1, если фактор несет положительный биологический смысл для системы, и b=1, если - отрицательный. Этот коэффициент имеет идентичные индексы (i=0,1,2) с функциями - возмущающими факторами fi. Такую же индексацию введем и для выходных функций yi.
Тогда запишем работу представленной биокибернетической схемы МБС.
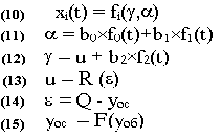
Жизнеспособность системы ограничена величиной , превышение которой на вход элементов БОУ приводит к его нарушению (разрушению): g > s .
Сформулируем функцию управляющего регулятора МБС. Вначале рассмотрим его работу в идеальной системе.
Предположим,
что внешние воздействия f(t) на
систему складываются из двух
частей: управления u(t), которое
можно генерировать по различным
биологическим законам, и
возмущения h(t), неподвластные
нашему влиянию.
(16) f(t) = u(t) + h(t).
Предположим также, что возмущение возможно достаточно точно описать какой-то комбинацией основных, "базисных" функций hi(t) с коэффициентом mi.
n
(17) h (t) = m1h1(t) +m2h2(t) + ... +m nhn(t) = еihi(t).
i=1
Цель
управления по-прежнему будет
состоять в выполнении
асимптотического соотношения:
(18) lim x(t) = 0.
t®Ґ
"Сконструируем"
управление в виде следующего
уравнения:
(19)
u(t) = u(t) + Du(t),
где u(t) - составляющая управления, которая стабилизирует систему в отсутствии возмущения (патологии); Du(t) - составляющая, признанная скомпенсировать" возмущение h(t).
В этом
случае стабилизирующая
составляющая управляющего
регулятора МБС представляет:
(20) u(t) = Q + f0(t) + f2(t).
При этом f2(t) следует рассматривать только как положительные эффекты (см. стр.131).
Для стабилизации системы, как следует из выше изложенного, при соблюдении условия (18) будет достаточным
n
(21) Du(t) = - h(t) - еhi(t).
i=1
Таким образом, решать задачу будет регулятор (19) и (20) при условии (18).
Такой "хороший" регулятор (идеальный регулятор для идеальной, но не реальной системы) имеет серьезный изъян: он требует точного знания коэффициентов разложения (m1,m2,..., mi) по выбранным функциям, отображающим биологические законы существования и работы МБС. Это уже практически второй изъян в описанном идеальном регуляторе. Первым недостатком все-таки следует признать, что описанный регулятор может работать только в условиях идеальной, замкнутой системы.
Все это не позволяет использовать такой регулятор в реальной БС в реальных условиях работы системы: при незнании коэффициентов m и к тому же при невозможности знать реальные параметры-входы функций МБС. Такие параметры невозможно определять даже в короткий временной промежуток t в силу их быстрой изменчивости.
В связи с этим требуется решать более сложную задачу - задачу об адекватном регуляторе в управлении МБС в условиях неопределенности.
Пусть имеется множество M, определяемое исключительно биологическим смыслом параметров. Выделим в этом множестве набор параметров управления y ( y I M ). Фактически этот набор y представляет (n+2)-мерный вектор.
Для решения этой задачи традиционным путем - идентифицировать y (получить точную оценку каждого из параметров), как следует из сути МБС, не представляется возможным. В этом случае требуется создать решающее правило L, согласно которому оценка и выработка управляющего сигнала не были разделены во времени и шли параллельно.
Возможность
такого решения подсказывает работа
В.А.Брусина [1], в которой приведено
решение управления механической
системой в условиях неполной
информации и неизвестности
параметров. При этом следует
учитывать ограниченность входных
параметров механической системы по
сравнению с МБС.
ЛИТЕРАТУРА
Смоленская государственная медицинская академия
Кафедра фармакологии
Поступила
в редакцию 15.01.97.